概述
什么是人工智能
人工智能(Artificial Intelligence)
使一部机器像人一样进行感知、认知、决策、执行的人工程序或系统
标志性事件

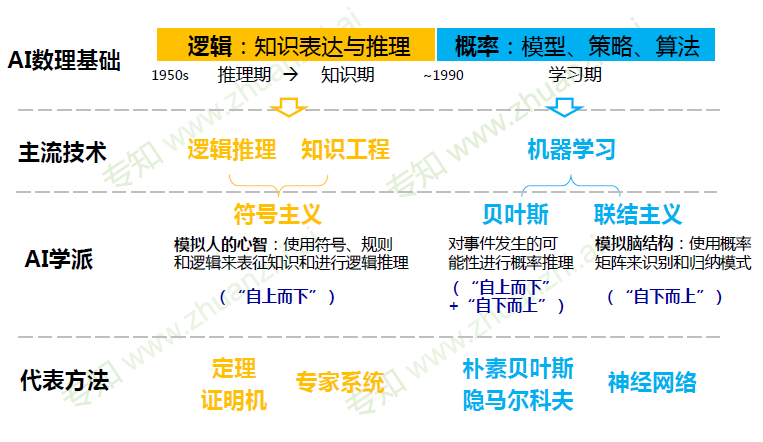
人工智能发展阶段

人工智能三个层面
计算智能
能存能算
感知智能
能听会说、能看会认
认知智能
能理解、会思考
人工智能 > 机器学习 > 深度学习
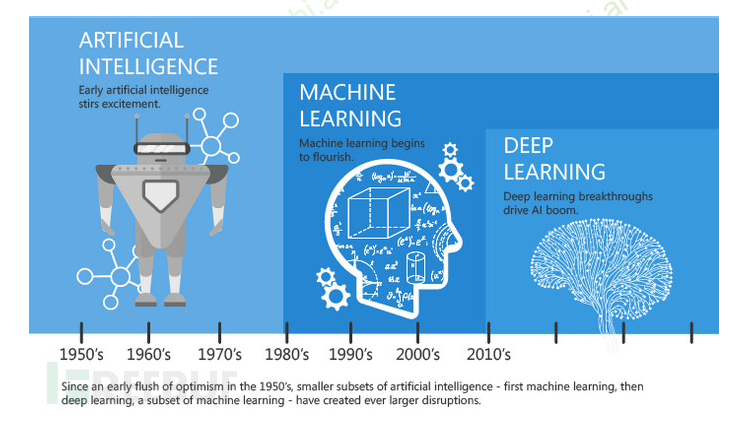
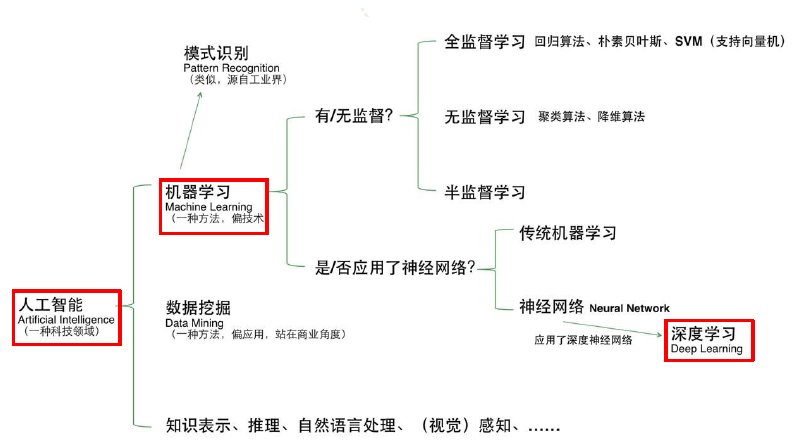
逻辑演绎 vs 归纳总结
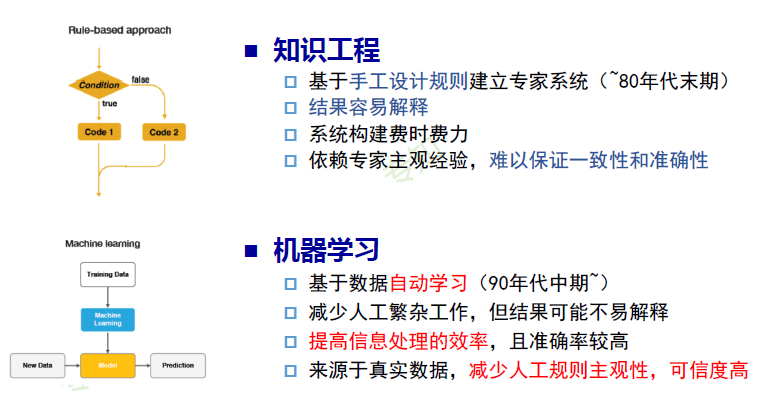
专家系统
根据专家定义的知识和经验,进行推理和判断,从而模拟人类专家的决策过程来解决问题。
知识工程 vs 机器学习
计算机视觉
人脸识别
图像分类
目标检测
图像搜索
图像分割
视频监控
语音技术
语音识别
语音合成
声纹识别
自然语言处理
文本分类
机器翻译
知识图谱
自动问答
信息检索
文本生成
机器学习的定义
最常用定义
计算机系统能够利用经验提高自身的性能
可操作定义
机器学习本质是一个基于经验数据的函数估计问题
统计学定义
提取重要模式、趋势,并理解数据,即从数据中学习
机器学习-怎么学
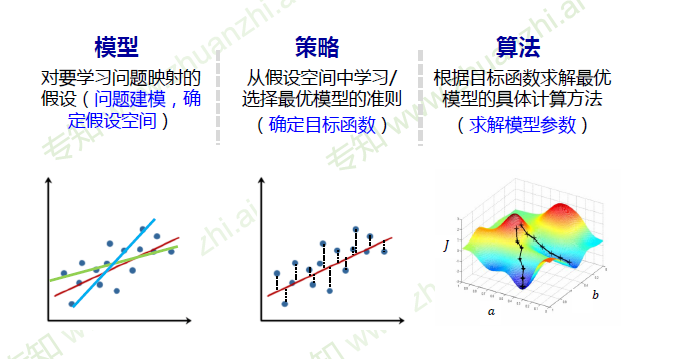
模型
对要学习问题映射的假设(问题建模,确定假设空间)
模型分类
数据标记
- 监督学习模型
- 无监督学习模型
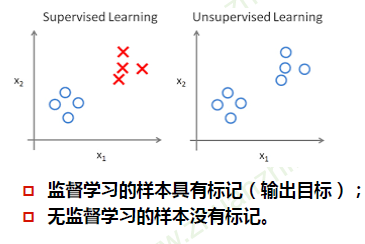
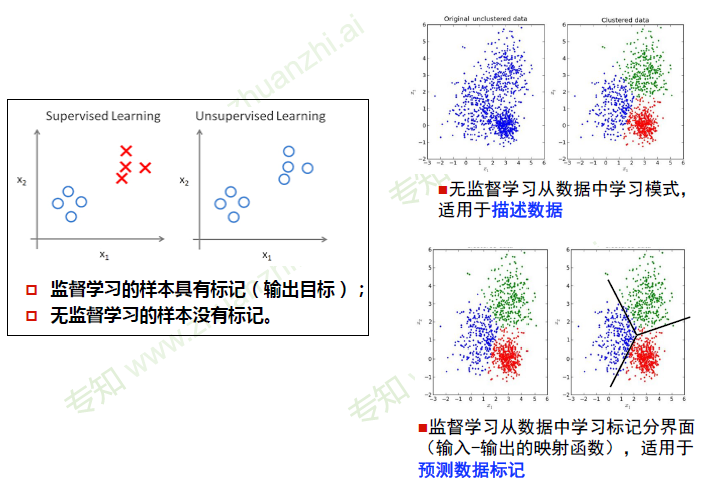
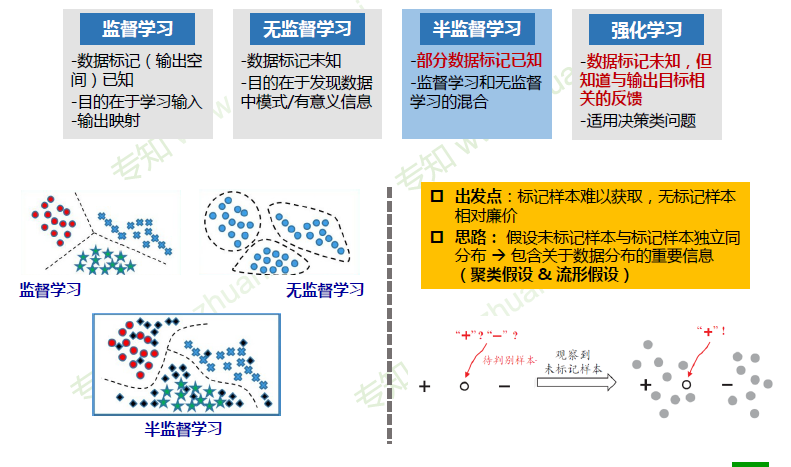
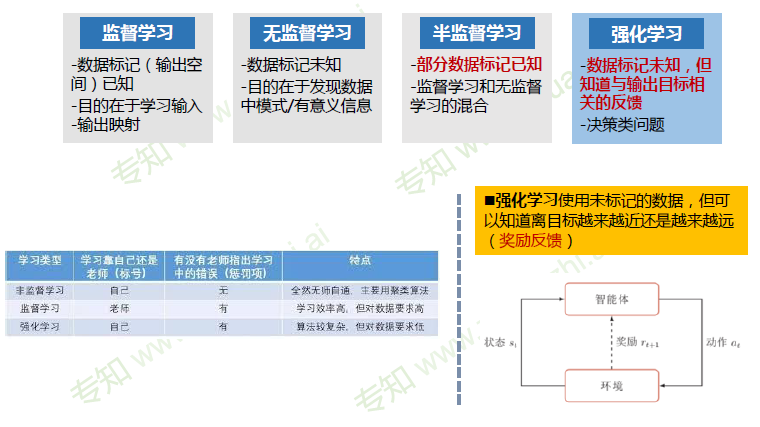
数据分布
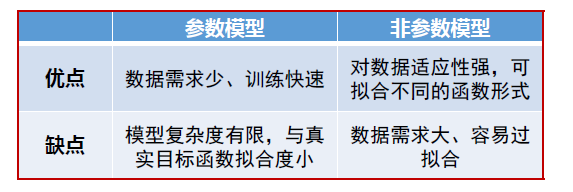
参数模型 、 无参数模型
建模对象
- 判别模型
- 生成模型

策略
从假设空间中学习/选择最优模型的准则
(确定目标函数)
算法
根据目标函数求解最优模型的具体计算方法
(求解模型参数)
深度学习
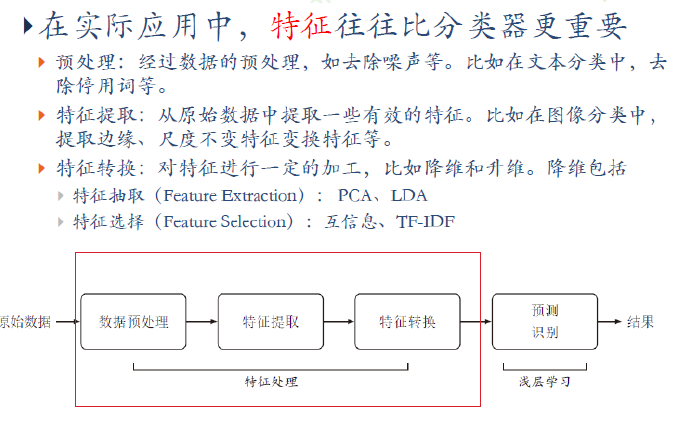
传统机器学习:人工设计特征
传统机器学习VS 深度学习
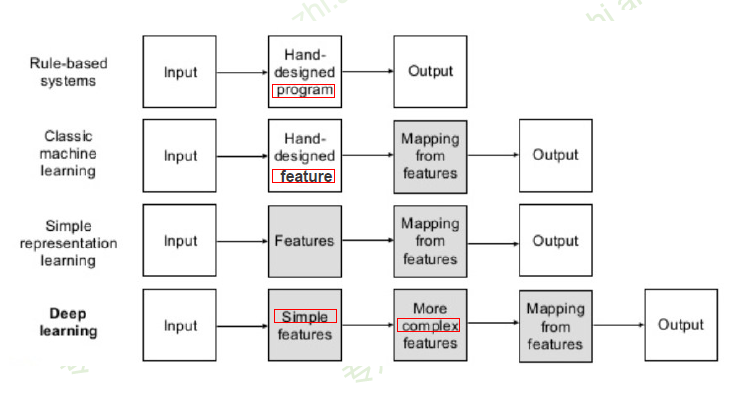
- 手动设计程序
- 手动设计特征
神经网络结构发展
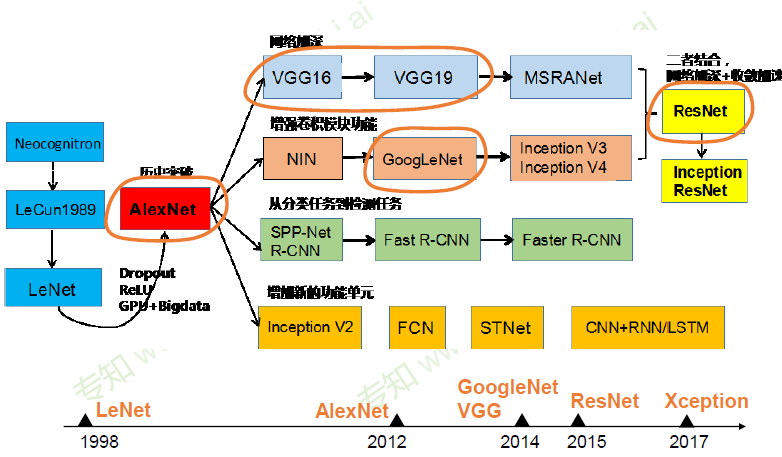
深度学习的不能

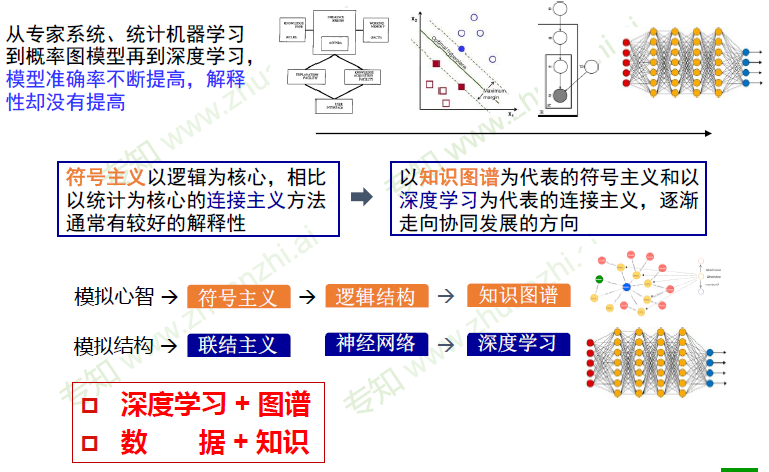
连接主义 vs 符号主义

- 从对立到合作
连接主义+ 符号主义
算法
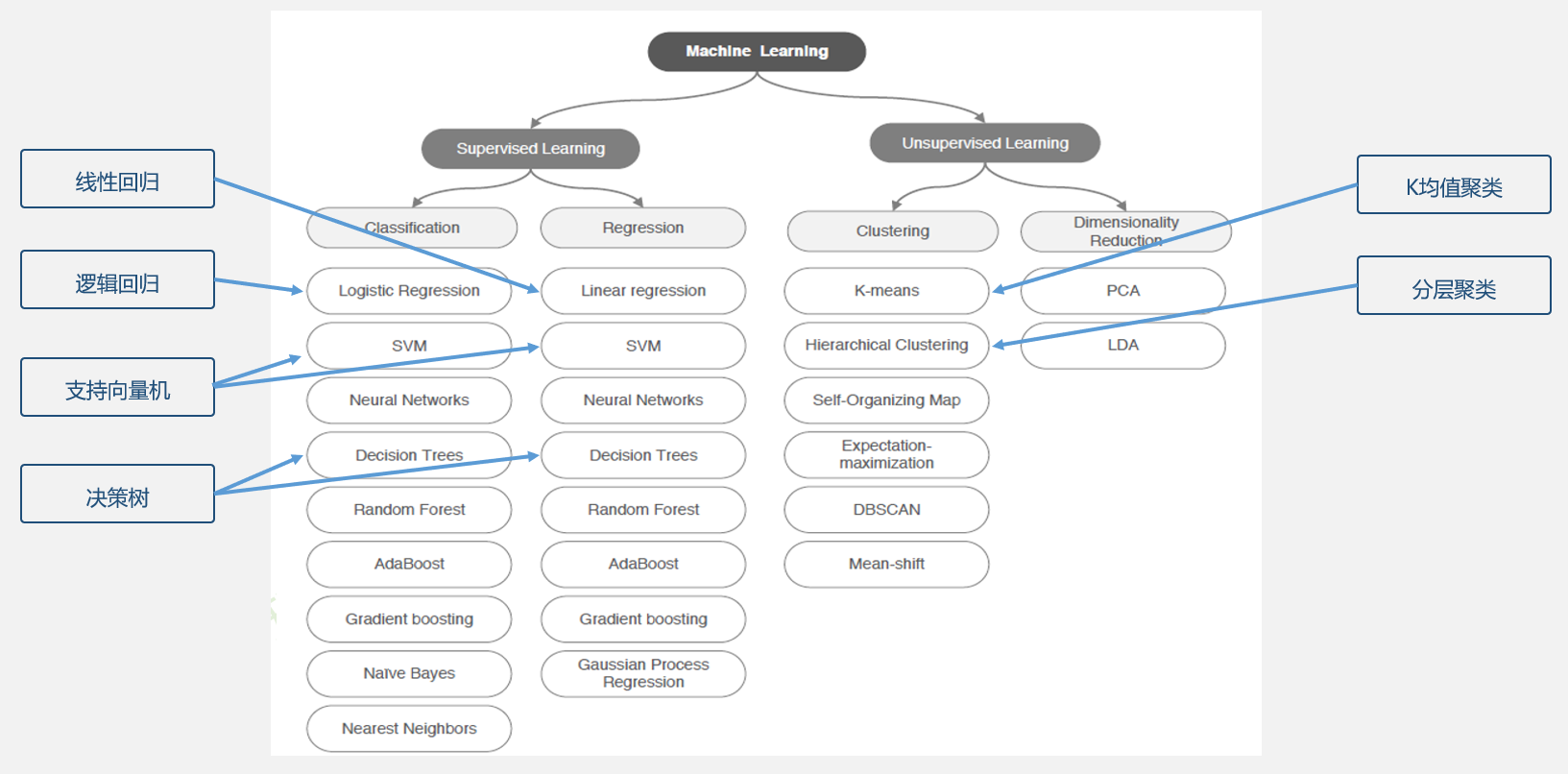
模型分类
根据有无监督,进行区分。对于有监督的情况,又可以分为分类和回归两类问题
定量输出称为回归,或者说是连续变量预测
定性输出称为分类,或者说是离散变量预测
无监督的情况下,有聚类和降维两种方法
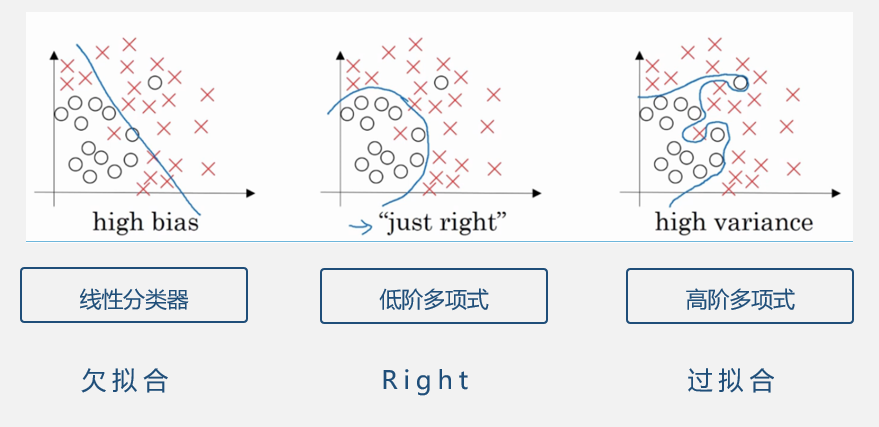
线性分类器
线性分类器就是用线性方程去拟合数据,在二维的情况下就是寻找一条直线,三维就是一个平面,更高维叫做超平面。寻找这个超平面的过程,其实就是求解所有权重参数的过程
学习过程

学习率
学习率低的话,学习过程会比较缓慢,学习率较高的话,学习过程更快,但是会更加跳跃。如果学习率过高的话,可能越过了好的分界面,得到了比较差的结果,但是如果训练集还足够多,可以通过后续的学习,弥补这一步产生的不良影响,重新找到好的分界面,但是整个学习过程更加曲折。在某些情况下,学习率也不是一成不变的。
第一种情况,可以根据训练集的大小来调整学习率,如将学习率乘上1/N,N代表训练集的大小
第二种情况,可以在每次迭代的过程中调整学习率,基本的思路是,需要朝着最优值移动的距离越远,学习率就应该越大,距离越近,学习率就应该更小。用自适应的方法来调整学习率。但是在实际中,可能并不知道和最优值之间的距离,所以可以在每一次迭代的最后,使用估计的模型参数检查误差函数。如果相对于上一次迭代,错误率减少了,可以增大学习率,用5%作为增大的幅度,如果相对于上一次迭代,错误率增大了,也就是跳过了最优值,那么应该重新设置上一轮迭代的权重wi,并且减少学习率到之前的50%
多项式分类器

过拟合
过拟合,高阶多项式为了避免犯任何错误,可能很深地切入了其他类的区域,会导致有些样本被错分
线性回归
一元线性回归和线性分类器类似,都是用一条直线去拟合数据,高维的情况也是一样,寻找一个超平面来拟合数据,目的都是求解出这个超平面方程,也就是求解出所有的参数wi,和常数项b
但是求解的过程不同,线性回归的求解过程是通过引入均方误差来实现的,均方误差代表样本中所有点到直线的距离之和,w、b的选取应该使均方误差达到最小。通过对w求偏导,可以直接导出w和b的结果。
过程:
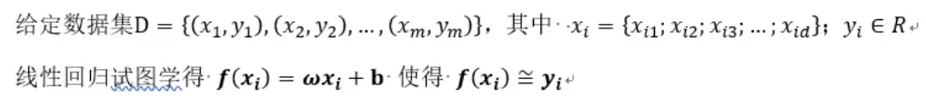
引入均方误差:
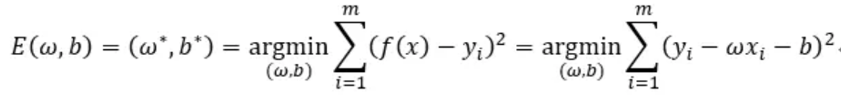
求解参数:
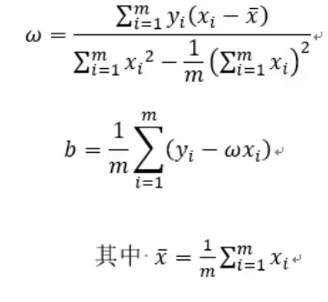
逻辑回归
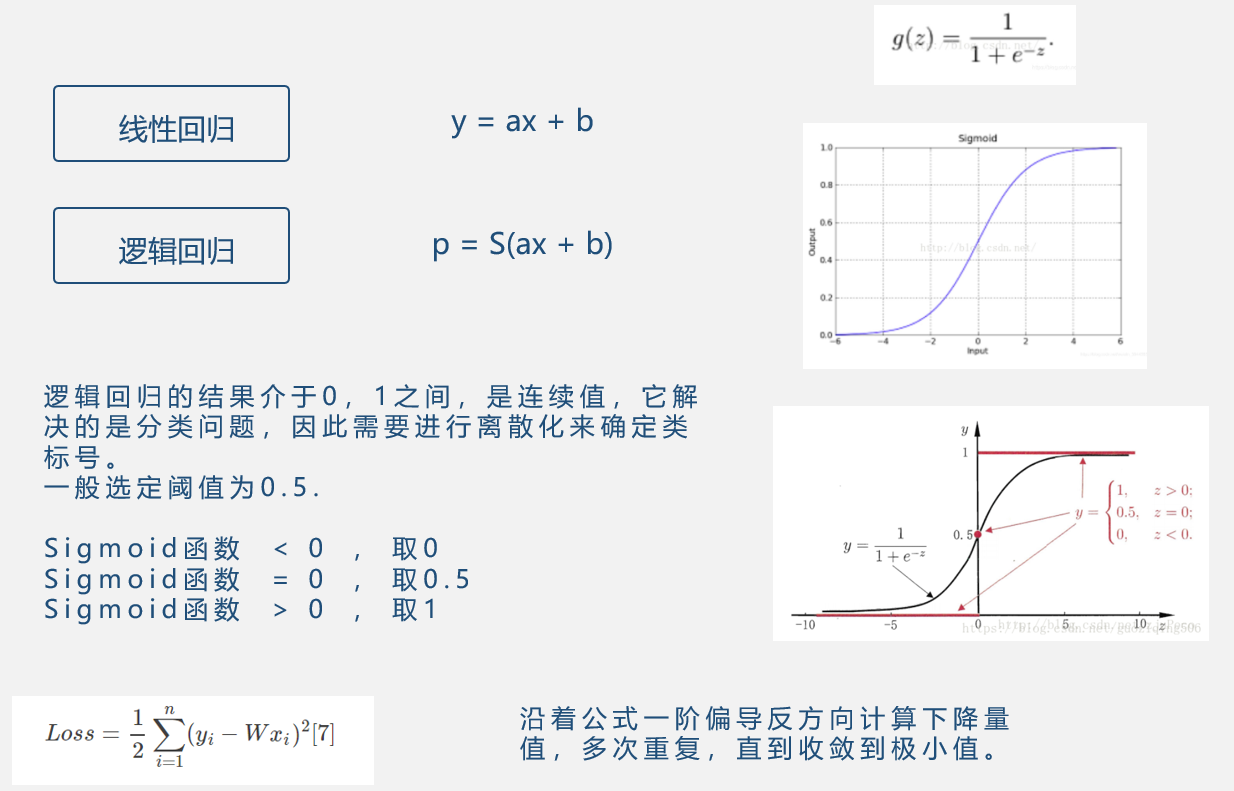
之所以叫逻辑回归,是因为用到了逻辑函数sigmoid,逻辑回归和svm有相似之处,都是根据已知的(xi,yi)这样的二元组,在空间上进行拟合,确定一条曲线,但是由于是分类问题,确定了曲线之后还需要阶跃函数,确定类标号,如果是二分类的话,根据(x,y)和曲线的位置关系,可以确定标号,阶跃函数为 z<0,0,z=0,0.5,z>0,1,但是这个函数是不连续的,不利于计算优化,所以取sigmiod函数作为阶跃函数,sigmiod函数在<0时取值大于0小于0.5,在>0时,取值大于0.5小于1,所以只需要比较和0.5的关系即可。z的值越大,表明元组的空间位置距离分类面越远,他就越可能属于类1,所以图中z越大,函数值也就越接近1;同理,z越小,表明元组越不可能属于类1。
与线性回归区别
逻辑回归用于分类,而不是回归。
线性回归模型中,输出一般是连续的,对于每一个x,都有一个对应的输出y。模型的定义域与值域都可以是无穷。
逻辑回归输入可以是连续的无穷,但是输出一般是离散的,通常只有{0,1}
支持向量机SVM
svm,支持向量机,既可用于回归又可用于分类
在深度学习出现之前,svm被认为是机器学习最好,最成功的算法
SVM是指将实例映射为二维中的点,以二分类举例的话,svm的目的就是画出一条线,来区分这两类点,理想的情况下,即使后来加入了新的点,这条线也能够进行很好的区分。理论上这条线有无数种画法,但他们有好坏的区分。期望的最理想的这条线叫做划分超平面,(叫做超平面是因为特征可能是高维的)。svm寻找可以区分两个类,并且使边际最大的超平面。边际指的是某一条线距离它两侧最近的点的距离之和。在边际最大的情况下,选取的平面应该是到两侧最近点距离相等的平面。
因为SVM要映射到高维空间,再来求分离超平面,但是这样的话,运算量会非常庞大,又因为上面的核函数和和映射到高维空间的解类似,所以求SVM分离超平面时,可以用求核函数方法代替在高维空间中计算,从而实现在一维平面上计算达到高维空间计算的效果

决策树

构建决策树
