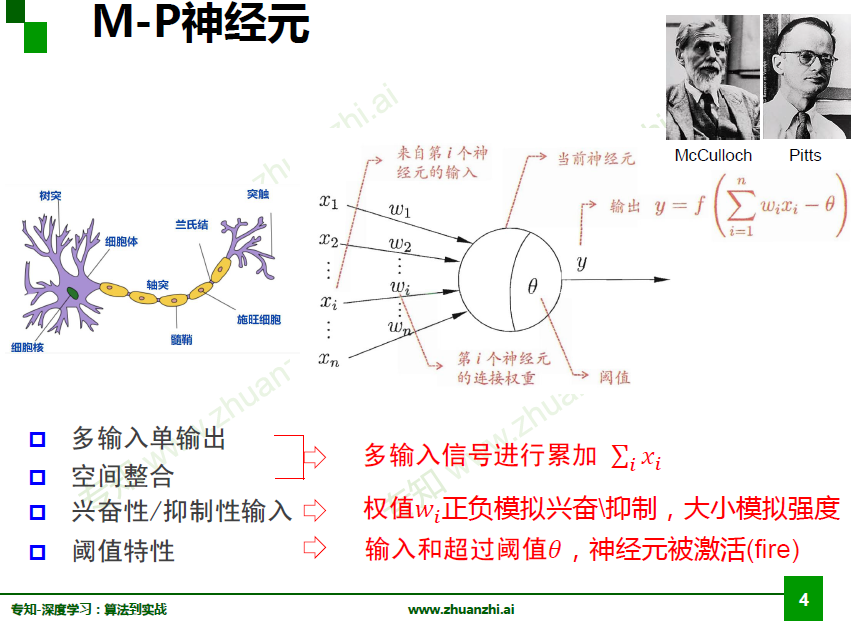
M-P神经元
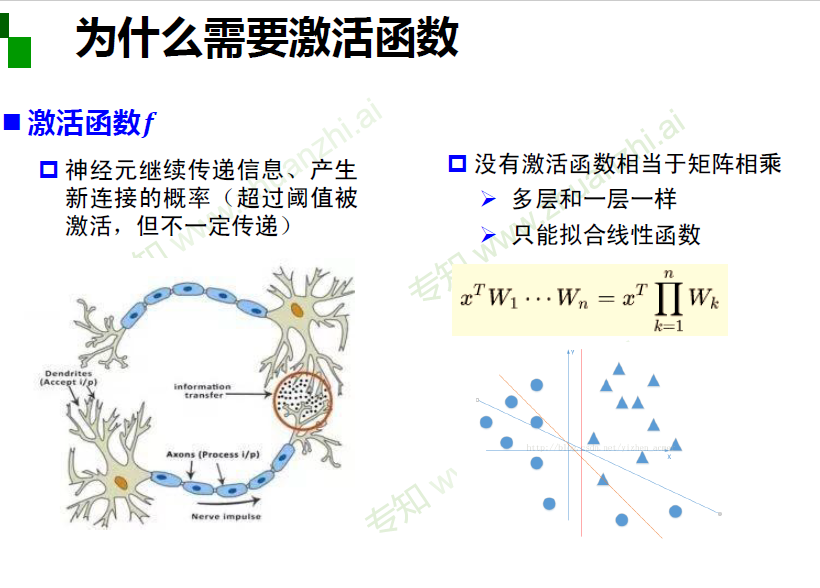
为什么需要激活函数
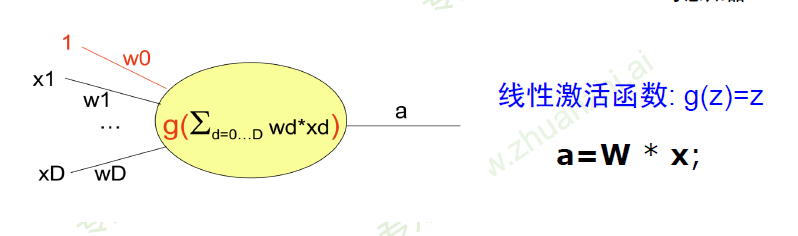
激活函数举例


权重人工设置
m-p神经元的权重由人工设置,无法学习
单层感知器
首个可以学习的神经网络
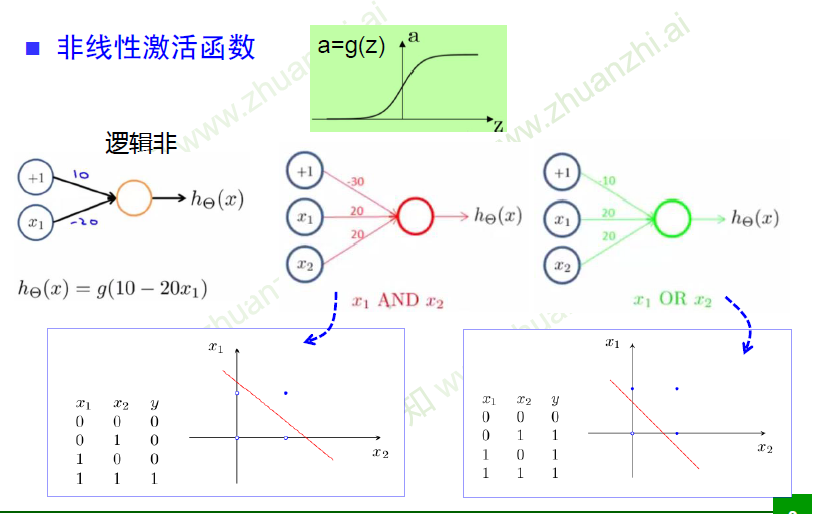
逻辑实现
多层感知器
异或
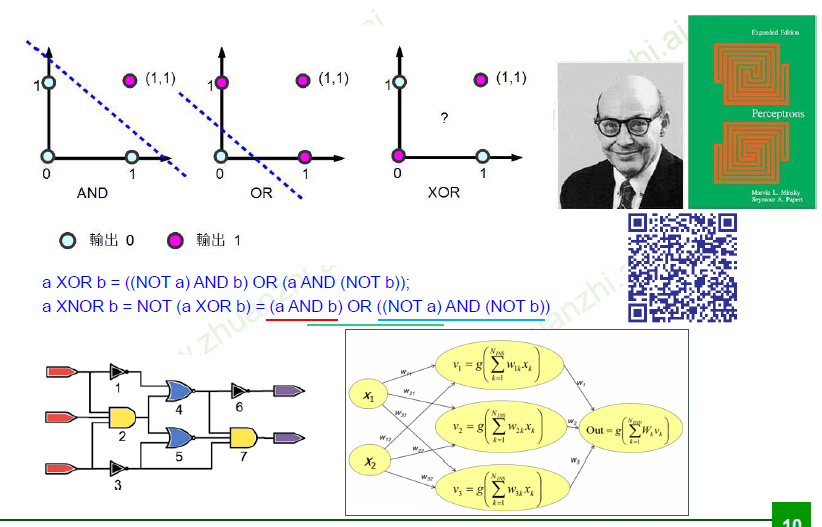
单层感知器,无法实现异或关系,无法找到一条线完美分开数据(0、1)
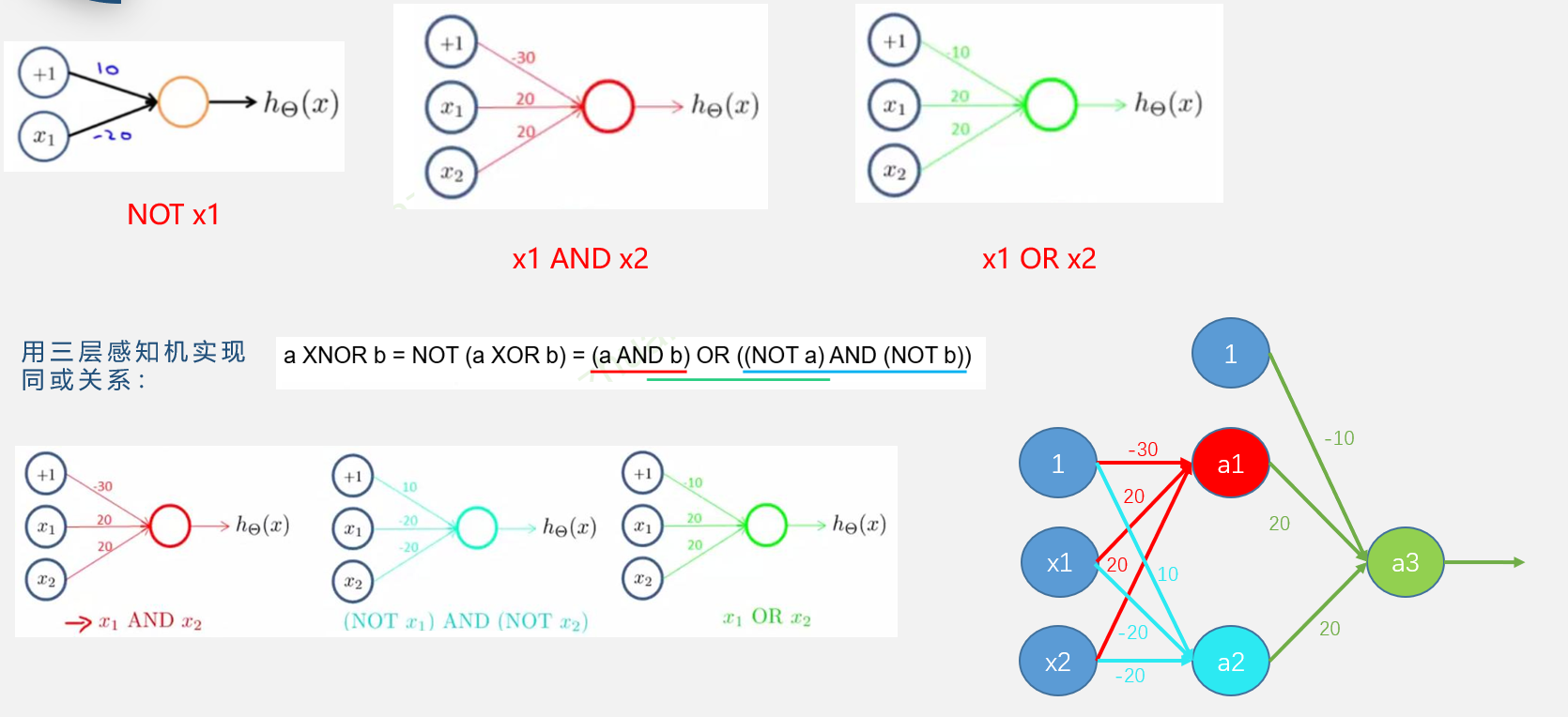
同或
三层感知机实现同或关系
单隐层神经网络可视化
url
http://playground.tensorflow.org/
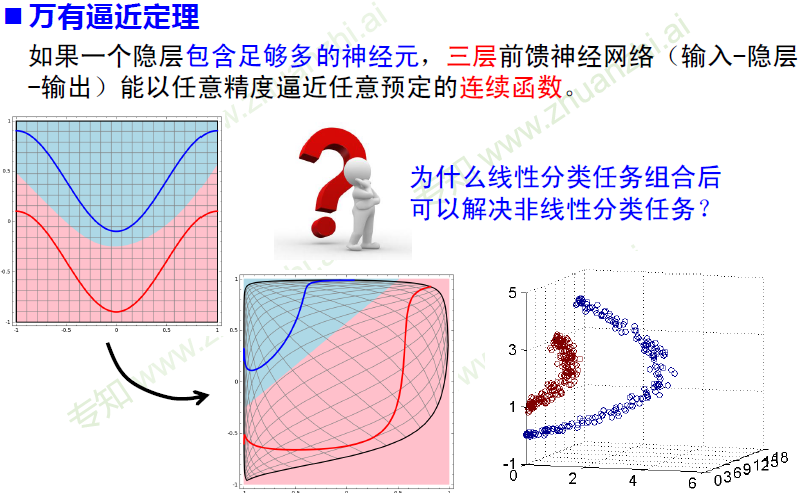
万有逼近定理
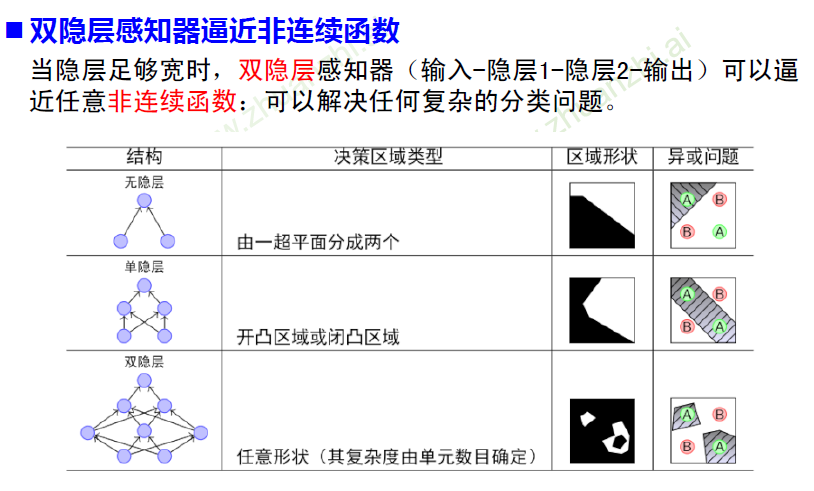
双隐层感知器
神经网络每一层作用
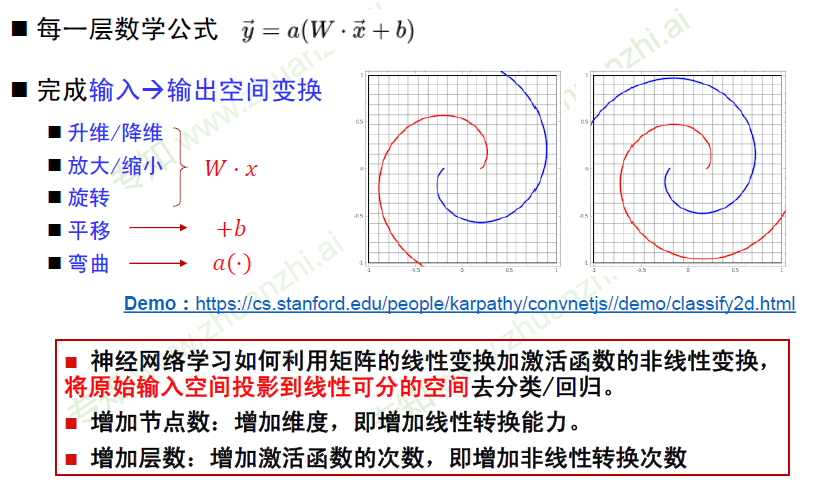
更深 or 更宽

误差反向传播
在训练神经网络的过程中,各个神经元的权重是通过误差的反向传播确定的,更新权重时,权重沿着误差函数梯度下降方向改变,使误差下降最快。
对于整个神经网络最后的误差来说,每一个神经元对于误差做出的贡献不同,如果激活函数选择sigmoid函数的话,输出层和隐层神经元的责任如图,计算出每个神经元的责任就可以将结果带入权重的更新公式,来调整权重。由于整个计算过程是从输出层开始,反向计算,所以也叫做误差的反向传播。


梯度消失
反向传播是误差沿着梯度方向反向传播,求偏导的过程中要计算激活函数的导数
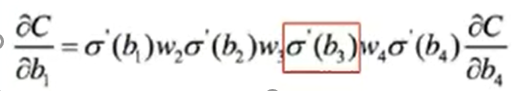
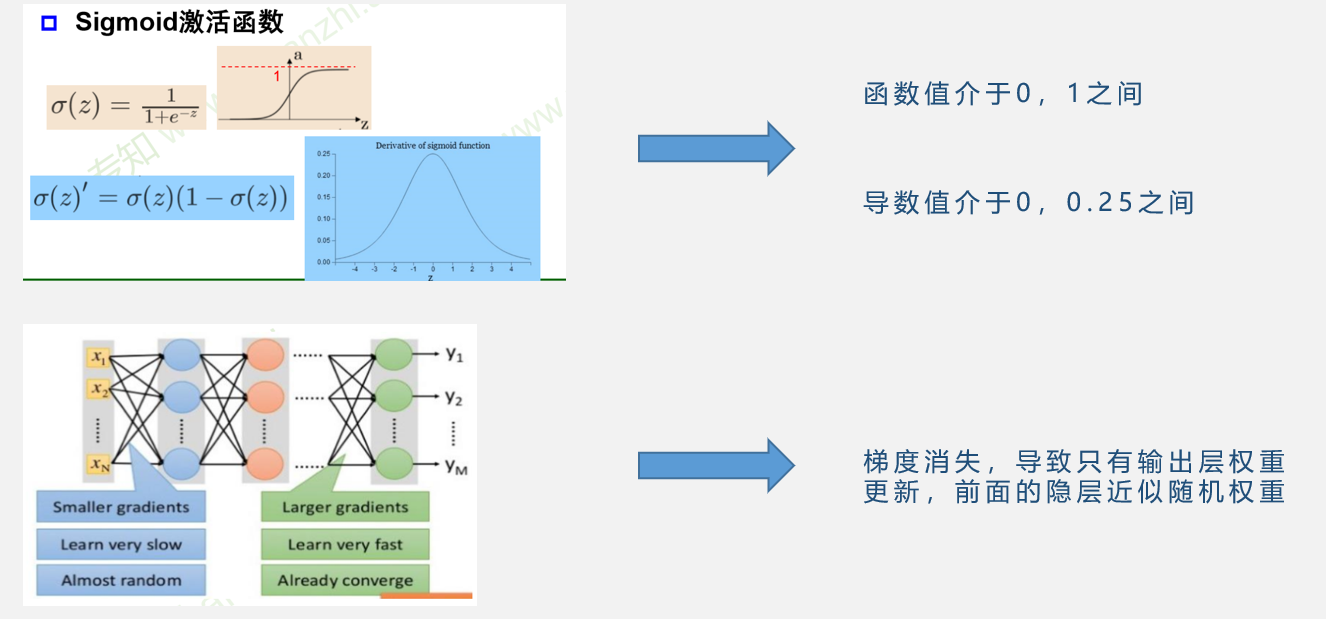
如果激活函数选择sigmoid函数的话,那么函数的导数值最大仅为4分之1,在1/2处取得,但很多情况下,函数值会落入饱和区,即sigmoid函数上下平滑的部分,这些地方的导数值可能会很小很小。而且这仅为一层网络,如果是多层网络的话,这个偏导值就会非常小,误差在反向传播的过程中就会消失,最后的结果可能是只改变了输出层的权重,而前面的网络权重都没有更新。
逐层预训练
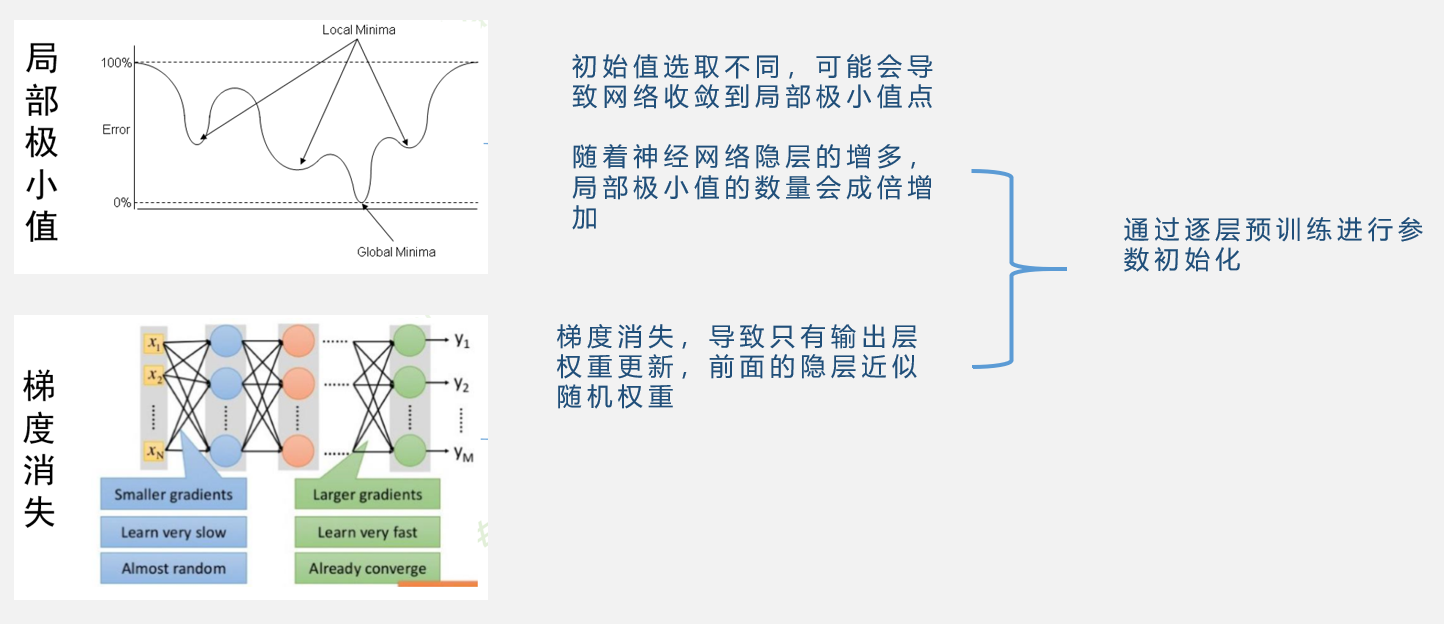
多层神经网络可能出现的两个问题,一是局部极小值,初始值选取不同,可能会导致网络收敛到局部极小值点,随着神经网络隐层的增多,局部极小值的数量会成倍增加。二就是梯度消失。
解决这两个问题的一个途径就是通过逐层预训练进行参数的初始化,如果参数的初始值选取得当,那么网络就会收敛到全局的极小值点,同时,由于梯度消失可能会导致前面几层网络权重无法更新,但是如果在开始的时候,就有一个较好的初始值,也可以使得网络训练出一个较好的结果。
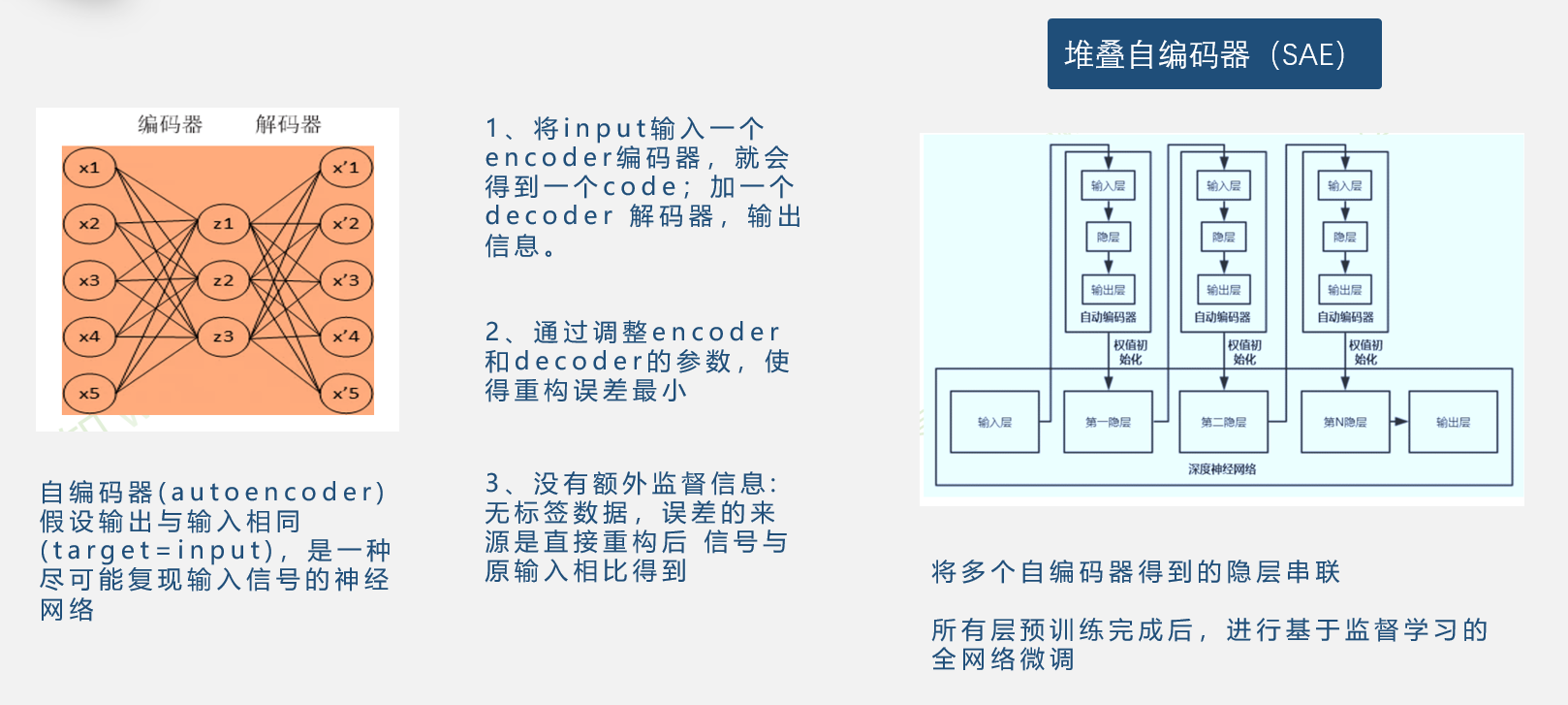
自编码器
逐层预训练是想得到一个好的初始值,但是如果网络有多个隐层,并不是每个隐层都能看到输出,也就是没有监督信息。在没有监督信息的情况下进行预训练主要有两种方法,自编码器和受限玻尔兹曼机。
自编码器假设输出与输入相同,是一种 尽可能复现输入信号的神经网络。
堆叠自编码器就是将多个自编码器进行串联,首先训练所有的隐层,在隐层训练完之后,通过输出层得到的监督结果,重新对整个网络进行微调
受限玻尔兹曼机
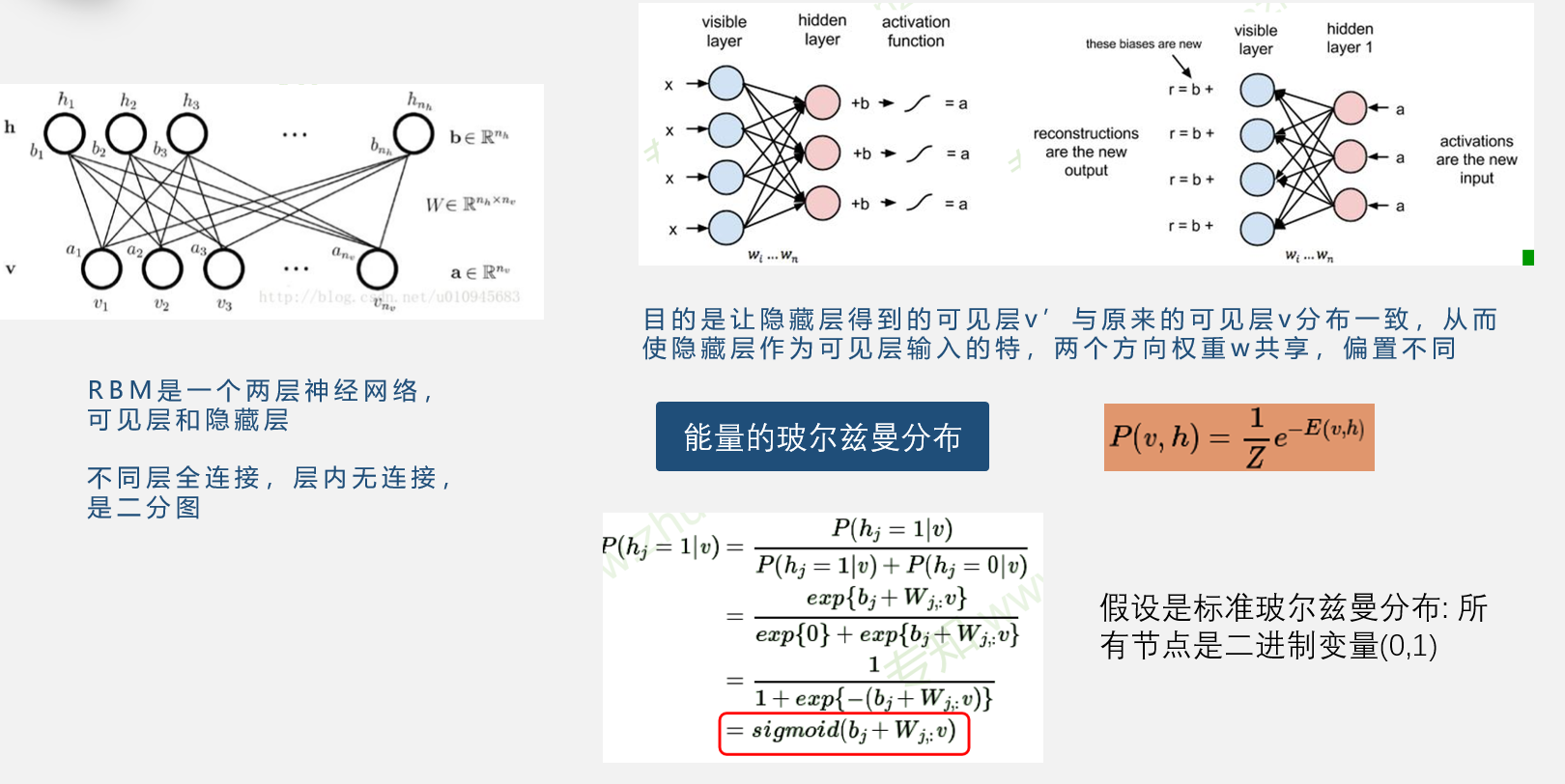
受限玻尔兹曼机是一个两层神经网络,包括可见层和隐藏层,不同层全连接,层内无连接,是二分图。
他的过程是首先通过可见层的输入,得到一个输出,再将输出传入隐藏层,重新得到一个可见层,在正向和反向的传播过程中,同一路线的权重相同,但是偏置不同。目的是让得到的可见层与原来的一致,这样就可以将隐藏层作为输入的一个特征,从而得到初始化。
之所以叫受限玻尔兹曼机是因为应用了热力学中的玻尔兹曼分布。巧合的是根据玻尔兹曼分布,假设所有的节点都用0,1二进制来表示,推导出的条件概率结果正好是sigmoid函数。
深度信念网络DBN
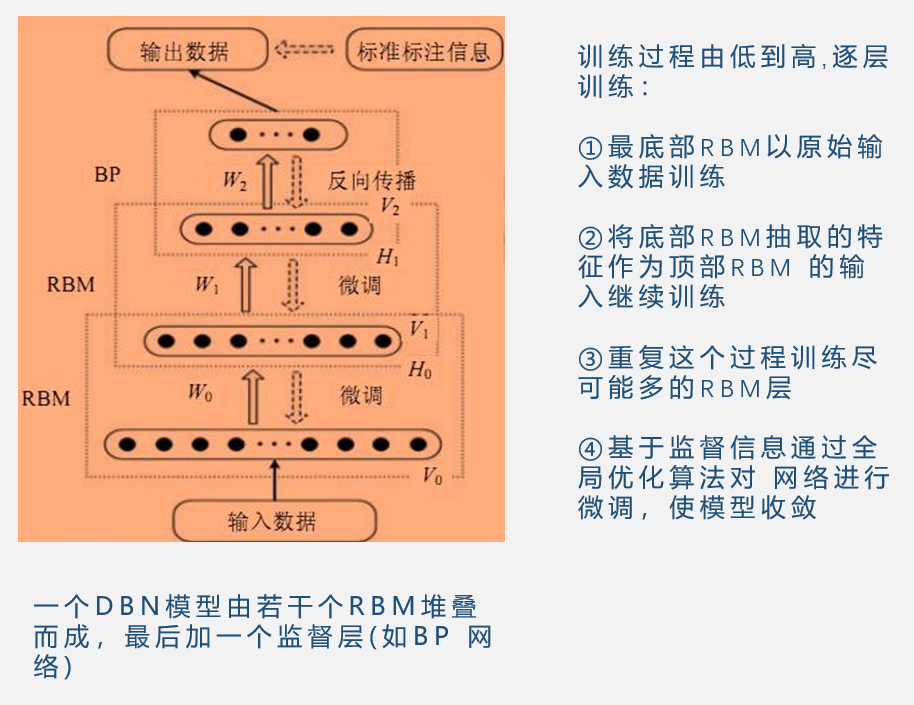
自编码器与RBM对比
| 自编码器 | RBM |
|---|---|
| 自编码器编码和解码函数不同 | RBM共享权重矩阵W,两个偏置向量 |
| 自编码器通过非线性变换学习特征,是确定的,特征值可以为任何实数 | RBM基于概率分布定义,高层表示为底层特征的条件概率,输出只有两种状态 (未激活激活),用二进制0/1表示 |
| 自编码器直接对条件概率 建模,是判别式模型 | RBM对联合概率密度建模, 是生成式模型 |
矩阵线性变换
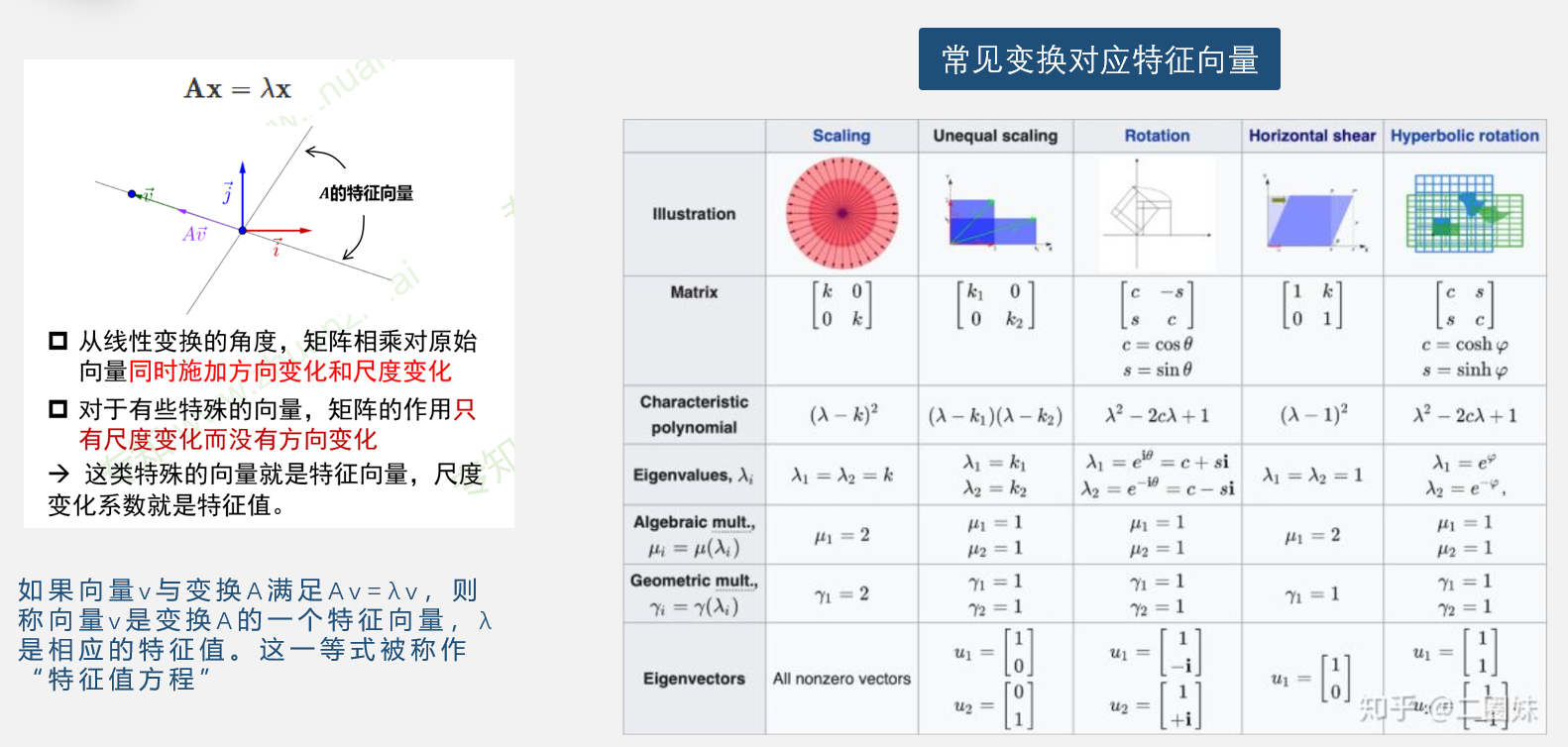
求解特征值、特征向量


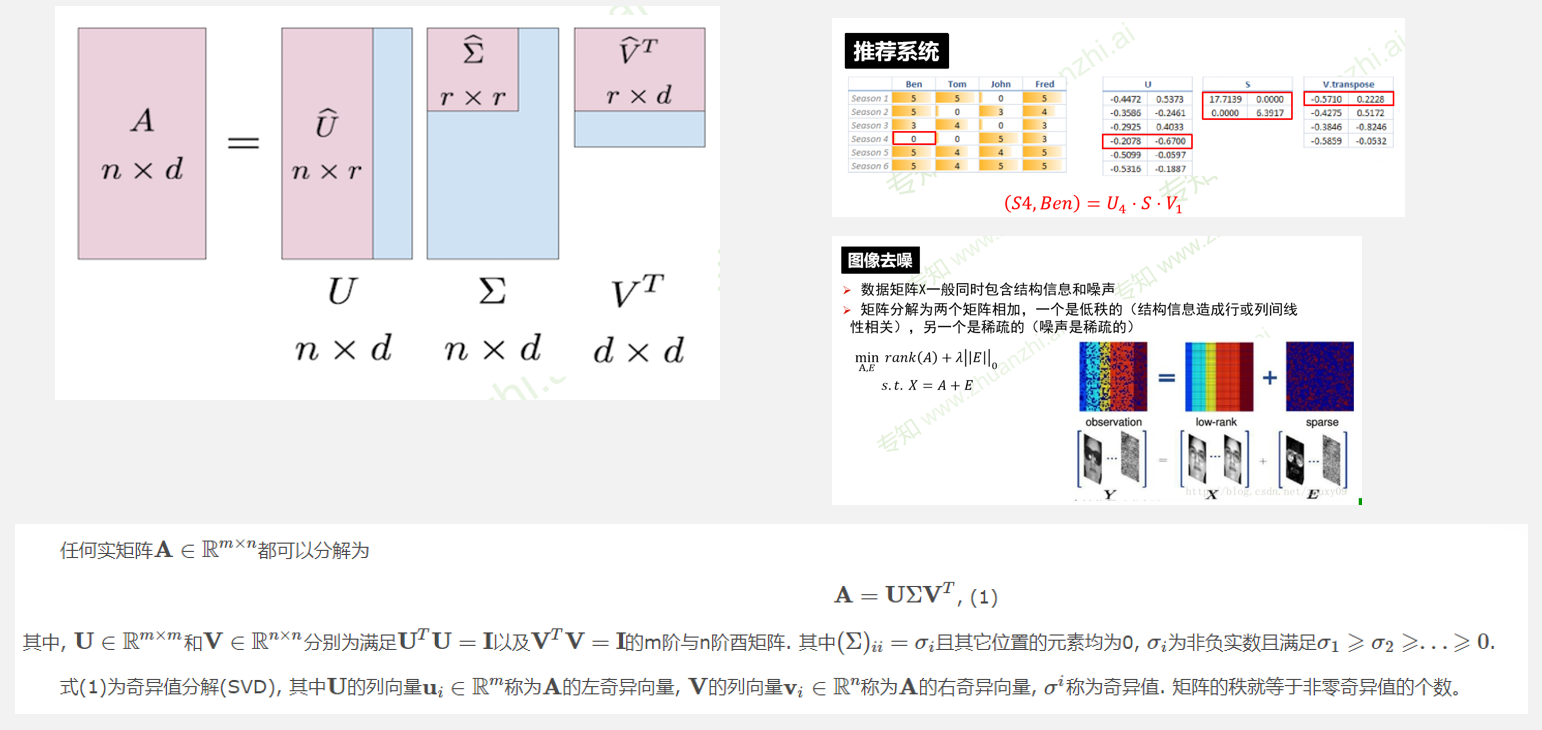
秩、奇异值与数据降维
方阵才有奇异矩阵和非奇异矩阵的概念
矩阵秩不为满秩则为奇异矩阵
矩阵行列式等于0,说明不满秩
设A为mn阶矩阵,q=min(m,n),A\A的q个非负特征值的算术平方根叫作A的奇异值。

奇异值标识着矩阵的“本质信息”,只保留奇异值分解之后奇异值更高的矩阵即可基本还原原始数据


奇异值分解与低秩近似
矩阵的低秩近似是一种稀疏表示形式,即利用一个秩较低的矩阵来近似表达原矩阵,不但能保留原矩阵的主要特征,而且可以降低数据的存储空间和计算复杂度
逻辑回归与最大似然
逻辑回归是分类任务,但采用了回归的方法,以二分类为例,如果采用线性回归的方法就是希望用一条直线将正负样例分开,由于直线的局限性,所以企图引入Sigmoid函数,从而引入曲线

确定函数形式之后,希望确定一组参数W,从而找到能够完成分类任务的曲线,从而引入最大似然估计
最大似然
概率描述的是在一定条件下某个事件发生的可能性,概率越大说明这件事情越可能会发生;而似然描述的是结果已知的情况下,该事件在不同条件下发生的可能性,似然函数的值越大说明该事件在对应的条件下发生的可能性越大
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我 们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。现在我们可以每次任意从已经摇匀的罐中拿一个球出来,记录球的颜色,然后把拿出来的球 再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?

因此在逻辑回归中,若想让预测出的结果全部正确的概率最大,根据最大似然估计,就是所有样本预测正确的概率相乘得到的P(总体正确)最大


频率学派与贝叶斯学派
