线性代数
特征值、特征向量


对角矩阵
矩阵相似
若矩阵$A$和矩阵$B$都是n阶矩阵,如果存在可逆矩阵$P$,使得 $P^{-1}AP=B$,则称$A$、$B$相似,记作$A\sim B$
矩阵相似对角化
如果一个n阶矩阵$A$有n个线性无关的特征向量,那么矩阵$A$与由其特征值所组成的对角矩阵($Λ$)相似,即: $A\simΛ$
对$A$的特征分解:
- 有一个NxN的矩阵$A$
- $A$有N个线性无关的特征向量($A\simΛ$)
- 由矩阵相似定义,则$P^{-1}AP=Λ$
- 两边同时左乘$P$,右乘$P^{-1}$,得到$A=PΛP^{-1}$
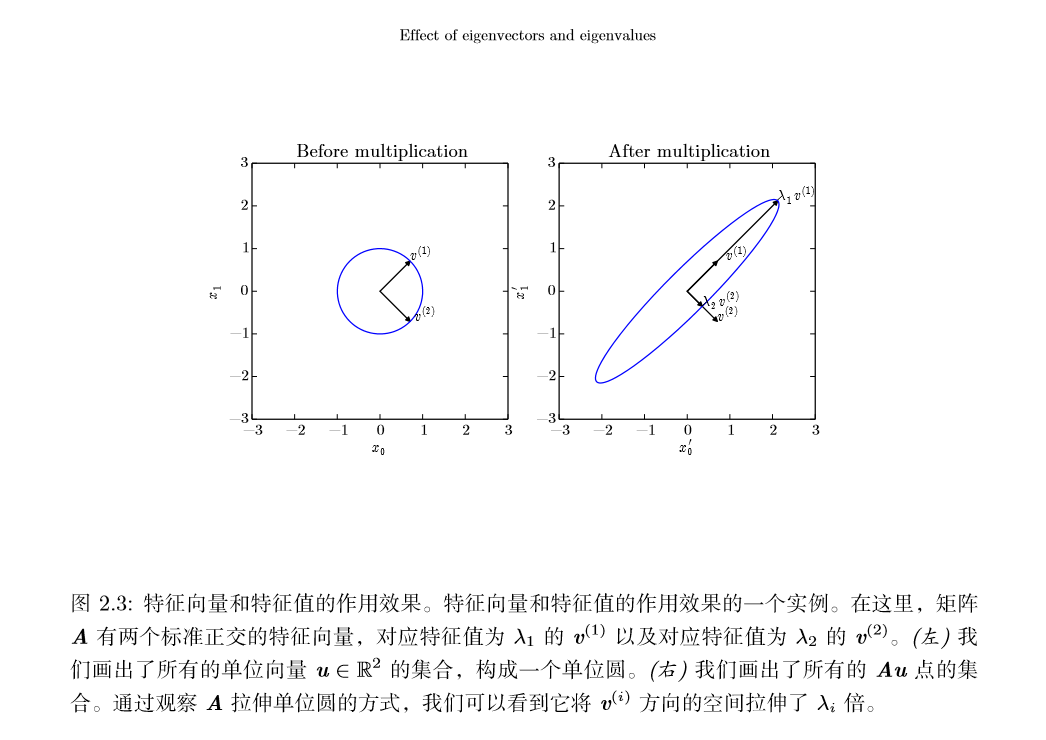
如果 $\upsilon$ 是$A$的特征向量,那么任何缩放后的向量 $s\upsilon\ (s∈R,s\neq0 ) $也是 $A$ 的 特征向量。此外,$s\upsilon$和 $\upsilon$ 有相同的特征值。基于这个原因,通常我们只考虑单位特征向量。
假设矩阵$A$有 n 个线性无关的特征向量 ${\upsilon^{(1)},…,\upsilon^{(n)}}$,对应着特征值 ${λ1,…,λn}$。我们将特征向量连接成一个矩阵,使得每一列是一个特征向量:$V = [\upsilon^{(1)},…,\upsilon^{(n)}]$类似地,我们也可以将特征值连接成一个向量 $λ =[λ1,…,λn]^⊤$。 因此$A$的特征分解(eigendecomposition)可以记作
我们将实对称矩阵分解成实特征向量和实特征值:
其中$Q$是$A$的特征向量组成的正交矩阵,$Λ$是对角矩阵,特征值$Λ_{i,i}$对应的特征向量是矩阵$Q$的第$i$列,记作$Q_{:,i}$,由于$Q$是正交矩阵,可以将$A$看作沿方向$v^{i}$延展$λ_{i}$倍的空间。
虽然任意一个实对称矩阵$A$都有特征分解,但是特征分解可能并不唯一。如果两个或多个特征向量拥有相同的特征值,那么在由这些特征向量产生的生成子空间中,任意一组正交向量都是该特征值对应的特征向量。因此,我们可以等价地从这 些特征向量中构成$Q$作为替代。按照惯例,我们通常按降序排列$Λ$的元素。在该 约定下,特征分解唯一当且仅当所有的特征值都是唯一的。
矩阵的特征分解给了我们很多关于矩阵的有用信息。矩阵是奇异的当且仅当含 有零特征值。
所有特征值都是正数的矩阵被称为正定(positive definite);所有特征值都是非 负数的矩阵被称为半正定(positive semidefinite)。同样地,所有特征值都是负数的 矩阵被称为负定(negative definite);所有特征值都是非正数的矩阵被称为 半负定 (negative semidefinite)。 半正定矩阵受到关注是因为它们保证 $∀x,x^{T}Ax≥0$。此外, 正定矩阵还保证$x^{T}Ax=0\Rightarrow x=0$。
矩阵的秩、奇异值、数据降维

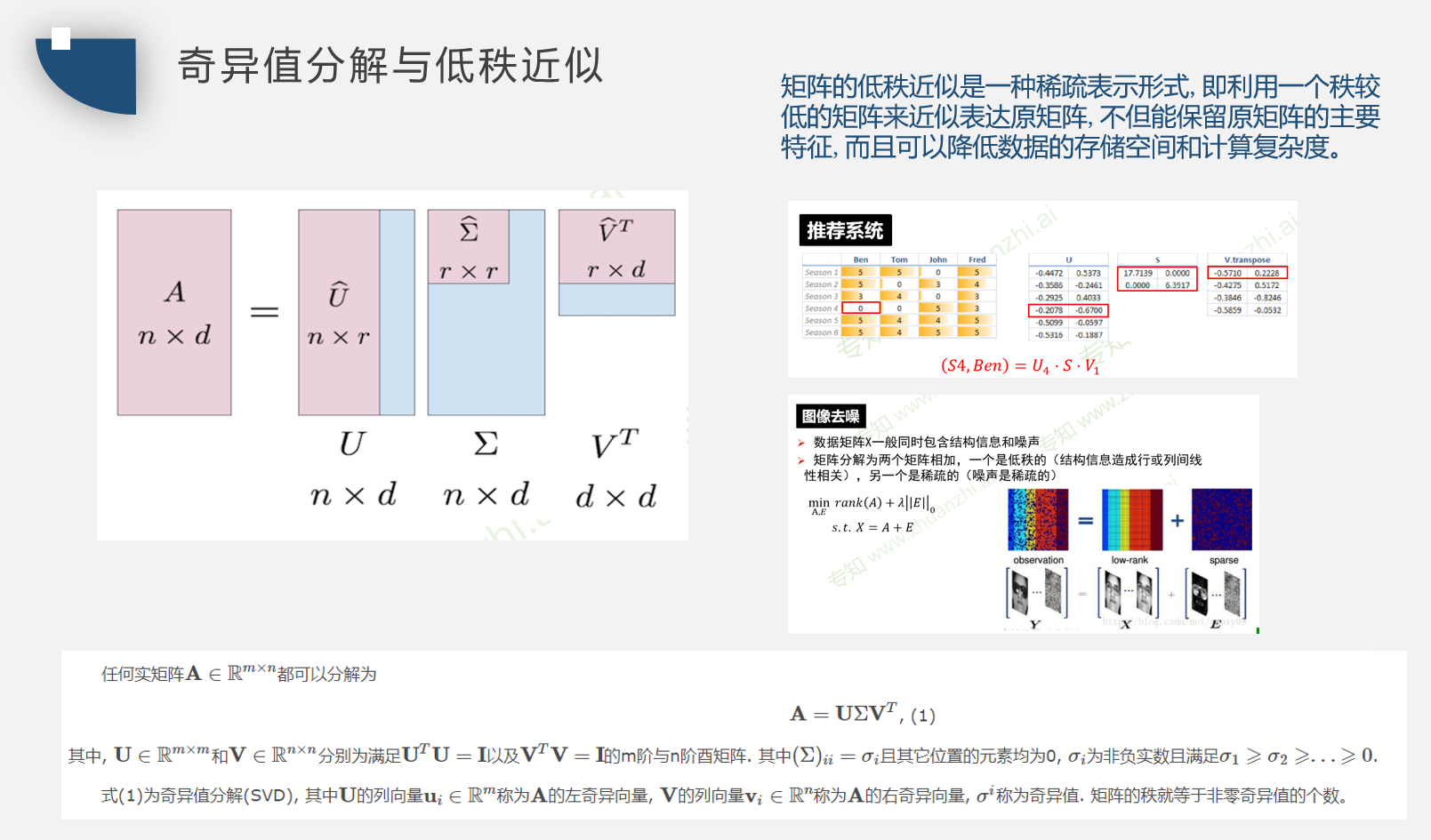
奇异值分解与低秩近似
奇异值分解
矩阵除了特征分解还有另一种分解方法,被称为奇异值分解(singular value decomposition, SVD),将矩阵分 解为奇异向量(singular vector)和奇异值(singular value)。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每 个实数矩阵都有一个奇异值分解,但不一定都有特征分解。例如,非方阵的矩阵没有特征分解,这时我们只能使用奇异值分解。
奇异值分解将矩阵$A$分解成三个矩阵的乘积:
假设$A$是一个 m×n 的矩阵,那么$U$是一个 m×m 的矩阵,$D$是一个 m×n 的矩阵,$V$是一个 n×n 矩阵。 这些矩阵中的每一个经定义后都拥有特殊的结构。矩阵$U$和$V$都定义为正交 矩阵,而矩阵$D$定义为对角矩阵。注意,矩阵$D$不一定是方阵。
对角矩阵$D$对角线上的元素被称为矩阵$A$的奇异值(singular value)。矩阵$U$的列向量被称为左奇异向量(left singular vector),矩阵$V$的列向量被称右奇异向量(right singular vector)。
事实上,我们可以用与$A$相关的特征分解去解释$A$的奇异值分解。$A$的左奇异向量(leftsingularvector)是$AA^{T}$的特征向量。$A$的右奇异向量(rightsingular vector)是$A^{T}A$的特征向量。$A$的非零奇异值是$A^{T}A$特征值的平方根,同时也是$AA^{T}$特征值的平方根。
SVD有用的一个性质可能是拓展矩阵求逆到非方矩阵上。
迹运算
迹运算返回的是矩阵对角元素的和:
迹运算有如下性质:
循环置换(将最后一个移到最前面):
对于标量a:
PCA
http://blog.codinglabs.org/articles/pca-tutorial.html
code
1 | def pca(dataMat, topNfeat=9999999): |
概率论
方差、协方差
协方差
协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远。如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于 取得相对较小的值,反之亦然。其他的衡量指标如相关系数(correlation)将每个变量的贡献归一化,为了只衡量变量的相关性而不受各个变量尺度大小的影响。
协方差和相关性是有联系的,但实际上是不同的概念。它们是有联系的,因为 两个变量如果相互独立那么它们的协方差为零,如果两个变量的协方差不为零那么 它们一定是相关的。然而,独立性又是和协方差完全不同的性质。两个变量如果协 方差为零,它们之间一定没有线性关系。独立性比零协方差的要求更强,因为独立 性还排除了非线性的关系。两个变量相互依赖但具有零协方差是可能的。例如,假 设我们首先从区间 [−1,1] 上的均匀分布中采样出一个实数 $x$。然后我们对一个随机变量 $s$ 进行采样。$s$ 以 $\frac{1}{2}$ 的概率值为 1,否则为-1。我们可以通过令 $y = sx$ 来生成 一个随机变量 $y$。显然,$x$ 和 $y$ 不是相互独立的,因为 $x$ 完全决定了 $y$ 的尺度。然 而,$Cov(x,y)=0$。
协方差矩阵
随机向量 $x∈R^{n}$ 的协方差矩阵(covariance matrix)是一个 n×n 的矩阵,并 且满足
协方差矩阵的对角元是方差:
分布
Beinoulli分布
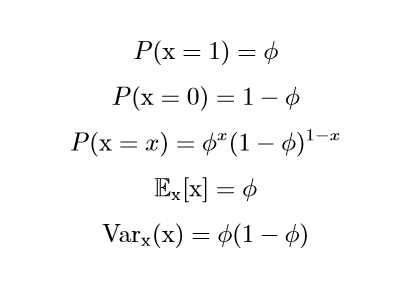
Multinoulli分布
Multinoulli 分布(multinoulli distribution)或者范畴分布(categorical distribution)是指在具有 $k$ 个不同状态的单个离散型随机变量上的分布,其中 $k$ 是一 个有限值。Multinoulli 分布由向量 $p∈ [0,1]^{k−1}$ 参数化,其中每一个分量 $p_i$ 表示 第 $i$ 个状态的概率。后的第 $k$ 个状态的概率可以通过 $1−1^⊤p$ 给出。注意我们必 须限制 $1^⊤p≤ 1$。Multinoulli 分布经常用来表示对象分类的分布,所以我们很少假设状态 1 具有数值 1 之类的。因此,我们通常不需要去计算 Multinoulli 分布的随机 变量的期望和方差
高斯分布
$µ$ 为中心峰值坐标,也是期望,标准差是σ
Dirac分布
Dirac delta 函数被定义成在除了在0取无穷,0以外的所有点的值都为 0,但是积分为 1。
高斯混合模型GMM
GMM是一种业界广泛使用的聚类算法,该方法使用了高斯分布作为参数模型,并使用了期望最大(Expectation Maximization,简称EM)算法进行训练,训练过程通过模型来计算数据的期望值。通过更新参数μ和σ来让期望值最大化。
首先分布概率是K个高斯分布的和,每个高斯分布有属于自己的$\mu$和$\sigma$参数,以及对应的权重参数,权重值必须为正数,所有权重的和必须等于1,以确保公式给出数值是合理的概率密度值 。
函数
logistic sigmoid
sigmoid函数通常用来产生Beinoulli分布中的参数$\phi$,因为范围是(0,1)
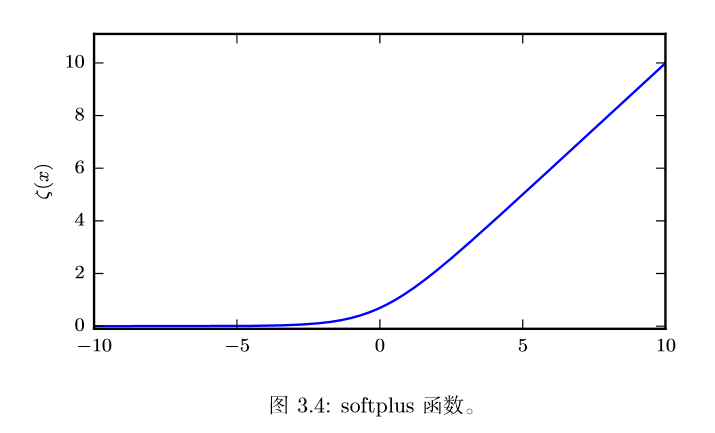
softplus
softplus可以用来产生正态分布的$\beta$和$\sigma$参数,因为范围是$(0,∞)$
性质
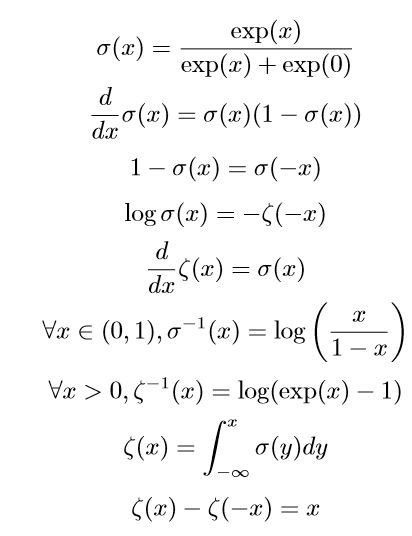
逻辑回归与最大似然


频率学派、贝叶斯

贝叶斯
贝叶斯公式
Pr(A)是A的先验概率或边缘概率。之所以称为”先验”是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率,也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率,也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率,也作标准化常量(normalized constant)。
意义
1 | 例如:一座别墅在过去的 20 年里一共发生过 2 次被盗,别墅的主人有一条狗,狗平均每周晚上叫 3 次,在盗贼入侵时狗叫的概率被估计为 0.9,问题是:在狗叫的时候发生入侵的概率是多少? |
信息论
信息论是应用数学的一个分支,主要研究的是对一个信号包含信息的多少进行量化。它初被发明是用来研究在一个含有噪声的信道上用离散的字母表来发送消息,例如通过无线电传输来通信。在这种情况下,信息论告诉我们如何对消息设计最优编码以及计算消息的期望长度,这些消息是使用多种不同编码机制、从特定的概率分布上采样得到的。在机器学习中,我们也可以把信息论应用于连续型变量, 此时某些消息长度的解释不再适用。信息论是电子工程和计算机科学中许多领域的基础。我们主要使用信息论的一些关键思想来描述概率分布或者量化概率分布之间的相似性。
量化信息的基本想法
- 非常可能发生的事件信息量要比较少,并且极端情况下,确保能够发生的事件应该没有信息量。
- 较不可能发生的事件具有更高的信息量。
- 独立事件应具有增量的信息。例如,投掷的硬币两次正面朝上传递的信息量, 应该是投掷一次硬币正面朝上的信息量的两倍
定义一个事件 x = $x$ 的自信息(self-information)为:
$I(x)$ 单 位是奈特(nats)。一奈特是以 $\frac{1}{e}$ 的概率观测到一个事件时获得的信息量。其他的材料中使用底数为 2 的对数,单位是比特(bit)或者香农(shannons);通过比特度量的信息只是通过奈特度量信息的常数倍。
当 x 是连续的,我们使用类似的关于信息的定义,但有些来源于离散形式的性质就丢失了。例如,一个具有单位密度的事件信息量仍然为 0,但是不能保证它一定 发生。
自信息只处理单个的输出。我们可以用香农熵(Shannon entropy)来对整个概 率分布中的不确定性总量进行量化:
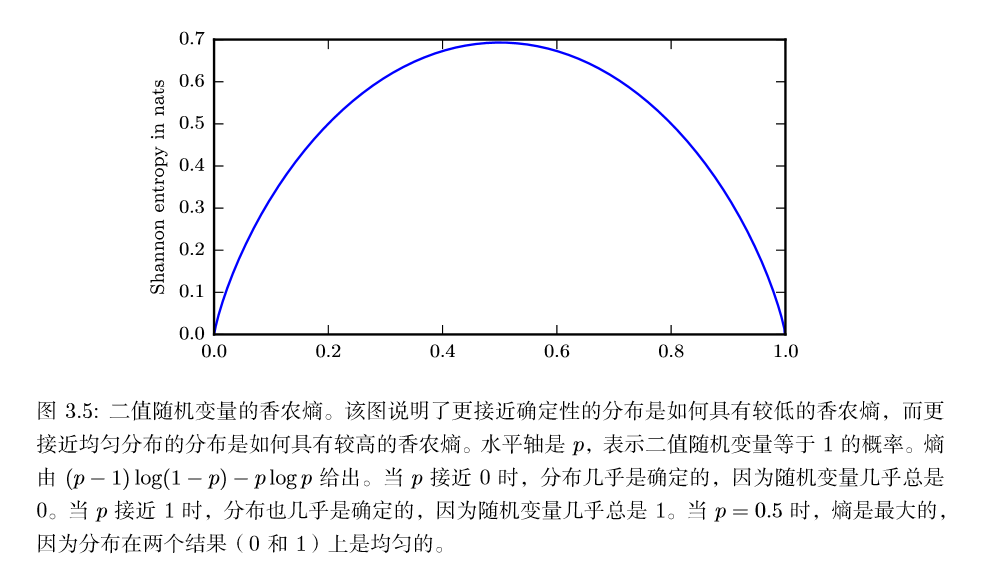
一个分布的香农熵是指遵循这个分布的事件所产生的期望信息总量。它给出了对依据概率分布 $P$ 生成的符号进行编码所需的比特数在平均意义上的下界 (当对数底数不是 2 时,单位将有所不同)。那些接近确定性的分布 (输出几 乎可以确定) 具有较低的熵;那些接近均匀分布的概率分布具有较高的熵。下图给出了一个说明。当x是连续的,香农熵被称为微分熵(differential entropy)。
KL散度
如果我们对于同一个随机变量 t 有两个单独的概率分布 $P(x)$ 和 $Q(x)$,我们可以使用KL 散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异
在离散型变量的情况下,KL 散度衡量的是,当我们使用一种被设计成能够使得概率分布$Q$产生的消息的长度最小的编码,发送包含由概率分布$P$产生的符号 的消息时,所需要的额外信息量 (如果我们使用底数为 2 的对数时,信息量用比特衡量,但在机器学习中,我们通常用奈特和自然对数。)
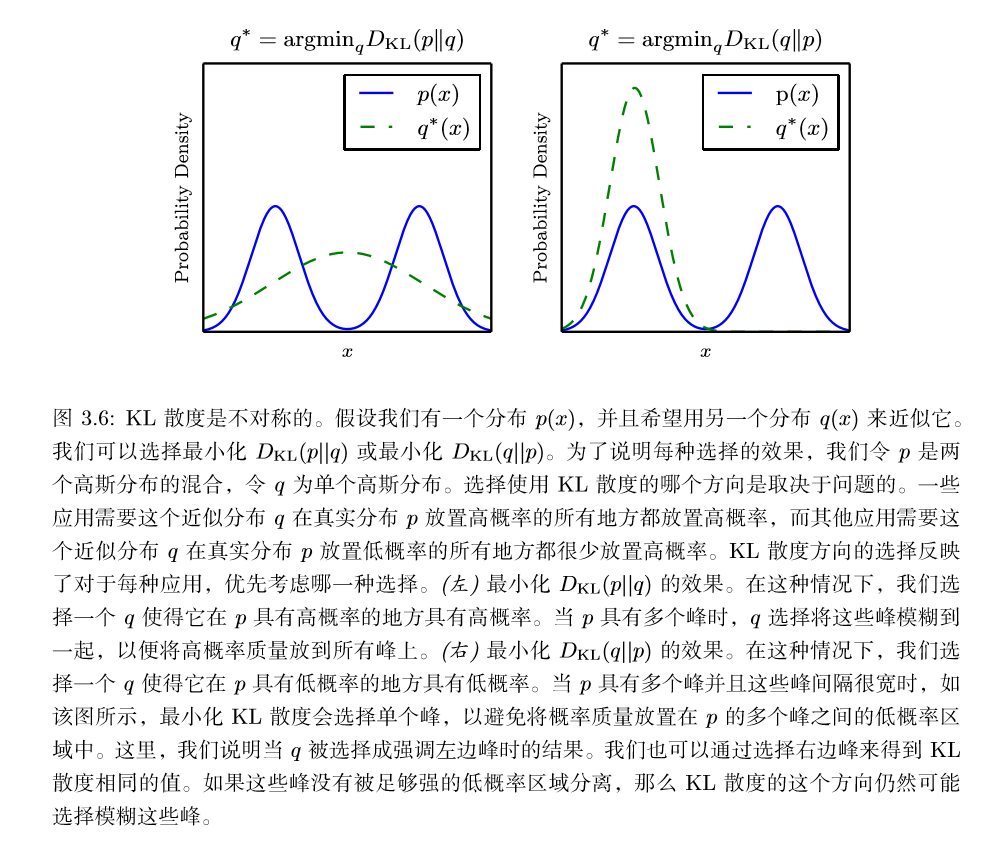
KL 散度有很多有用的性质,最重要的是它是非负的。KL 散度为 0 当且仅当$P$和$Q$在离散型变量的情况下是相同的分布,或者在连续型变量的情况下是 ‘‘几乎处处’’ 相同的。因为 KL 散度是非负的并且衡量的是两个分布之间的差异,它经常被用作分布之间的某种距离。然而,它并不是真的距离因为它不是对称的:对于某 些$P$和$Q$,$D_{KL}(P||Q)\neq D_{KL}(Q||P)$。这种非对称性意味着选择$D_{KL}(P||Q)$ 还是$D_{KL}(Q||P)$ 影响很大
一个和 KL 散度密切联系的量是交叉熵(cross-entropy)$H(P,Q)=H(P)+ D_{KL}(P||Q)$,它和 KL 散度很像但是缺少左边一项:
针对 $Q$ 最小化交叉熵等价于最小化 KL 散度,因为 $Q$ 并不参与被省略的那一项。
当我们计算这些量时,经常会遇到 $0log0$ 这个表达式。按照惯例,在信息论中, 我们将这个表达式处理为 $lim_{x\rightarrow0}xlogx=0$