NLP一

Veröffentlicht am | Edited on | in . | Views:

NLP

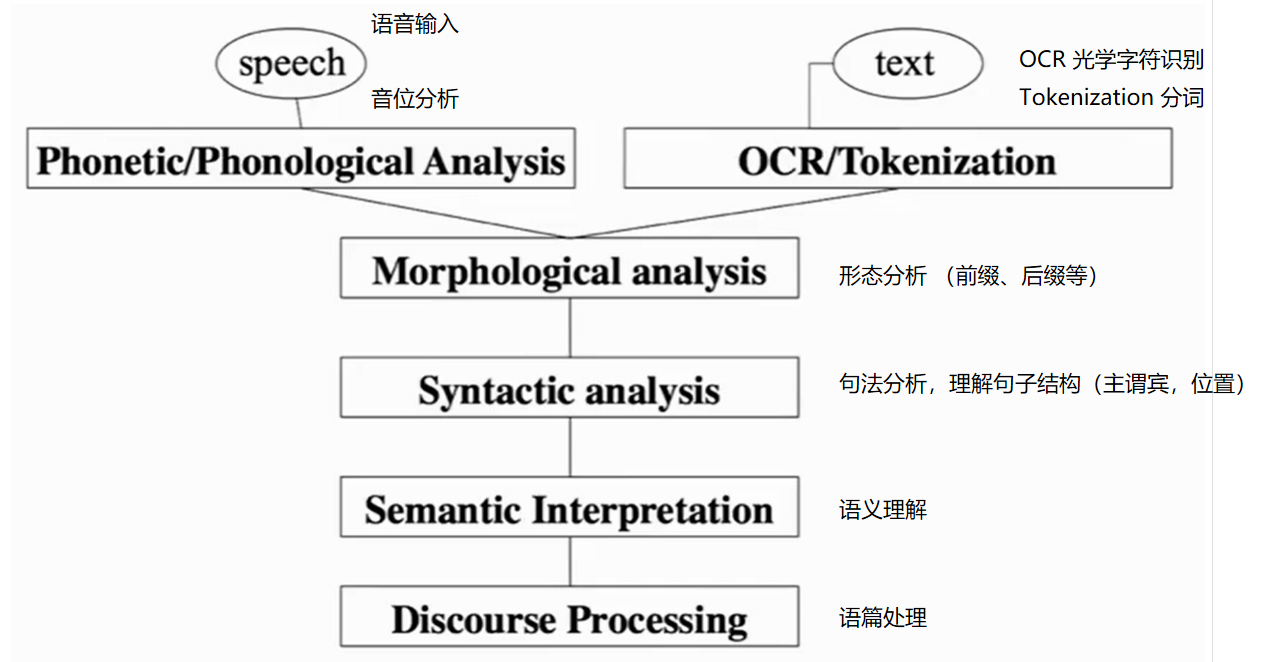
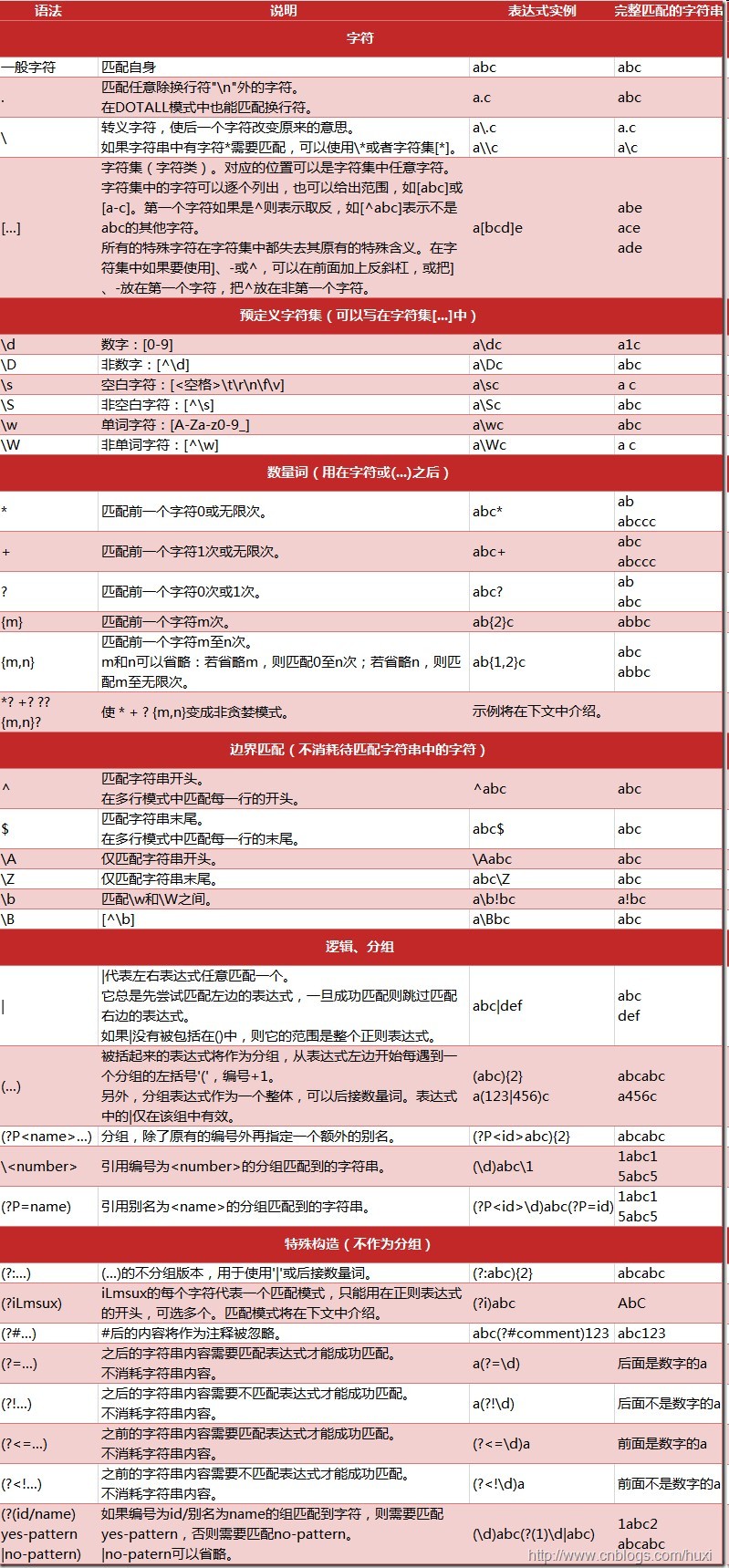
正则表达式

验证工具：http://regexr.com/

练习地址： https://alf.nu/RegexGolf 

1
2
3
4
5
6
7
8
9
10
11
import re
 
# 将正则表达式编译成Pattern对象
pattern = re.compile(r'hello.*\!')
 
# 使用Pattern匹配文本，获得匹配结果，无法匹配时将返回None
match = pattern.match('hello, hanxiaoyang! How are you?')
 
if match:
    # 使用Match获得分组信息
    print match.group()

jieba

jieba一般用来完成中文分词

jieba.cut 以及 jieba.cut_for_search 返回的结构都是一个可迭代的 generator 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import jieba

seg_list = jieba.cut("我在学习自然语言处理", cut_all=True)
print seg_list
print("Full Mode: " + "/ ".join(seg_list))  # 全模式

seg_list = jieba.cut("我在学习自然语言处理", cut_all=False)
print("Default Mode: " + "/ ".join(seg_list))  # 精确模式

seg_list = jieba.cut("他毕业于上海交通大学，在百度深度学习研究院进行研究")  # 默认是精确模式
print(", ".join(seg_list))

seg_list = jieba.cut_for_search("小明硕士毕业于中国科学院计算所，后在哈佛大学深造")  # 搜索引擎模式
print(", ".join(seg_list))

'''
Full Mode: 我/ 在/ 学习/ 自然/ 自然语言/ 语言/ 处理
Default Mode: 我/ 在/ 学习/ 自然语言/ 处理
他, 毕业, 于, 上海交通大学, ，, 在, 百度, 深度, 学习, 研究院, 进行, 研究
小明, 硕士, 毕业, 于, 中国, 科学, 学院, 科学院, 中国科学院, 计算, 计算所, ，, 后, 在, 哈佛, 大学, 哈佛大学, 深造
'''

jieba.lcut以及jieba.lcut_for_search直接返回 list 

1
2
3
4
5
6
7
8
9
10
result_lcut = jieba.lcut("小明硕士毕业于中国科学院计算所，后在哈佛大学深造")
print result_lcut
print " ".join(result_lcut)
print " ".join(jieba.lcut_for_search("小明硕士毕业于中国科学院计算所，后在哈佛大学深造"))

'''
[u'\u5c0f\u660e', u'\u7855\u58eb', u'\u6bd5\u4e1a', u'\u4e8e', u'\u4e2d\u56fd\u79d1\u5b66\u9662', u'\u8ba1\u7b97\u6240', u'\uff0c', u'\u540e', u'\u5728', u'\u54c8\u4f5b\u5927\u5b66', u'\u6df1\u9020']
小明 硕士 毕业 于 中国科学院 计算所 ， 后 在 哈佛大学 深造
小明 硕士 毕业 于 中国 科学 学院 科学院 中国科学院 计算 计算所 ， 后 在 哈佛 大学 哈佛大学 深造
'''

添加用户自定义字典

很多时候我们需要针对自己的场景进行分词，会有一些领域内的专有词汇。

  • 1.可以用jieba.load_userdict(file_name)加载用户字典
  • 2.少量的词汇可以自己用下面方法手动添加：
    • 用 add_word(word, freq=None, tag=None) 和 del_word(word) 在程序中动态修改词典
    • 用 suggest_freq(segment, tune=True) 可调节单个词语的词频，使其能（或不能）被分出来。
1
2
3
4
5
6
7
8
print('/'.join(jieba.cut('如果放到旧字典中将出错。', HMM=False)))
# 如果/放到/旧/字典/中将/出错/。

jieba.suggest_freq(('中', '将'), True)
# 494

print('/'.join(jieba.cut('如果放到旧字典中将出错。', HMM=False)))
# 如果/放到/旧/字典/中/将/出错/。

关键词提取

基于 TF-IDF 算法的关键词抽取

import jieba.analyse

  • jieba.analyse.extract_tags(sentence, topK=20, withWeight=False, allowPOS=())
    • sentence 为待提取的文本
    • topK 为返回几个 TF/IDF 权重最大的关键词，默认值为 20
    • withWeight 为是否一并返回关键词权重值，默认值为 False
    • allowPOS 仅包括指定词性的词，默认值为空，即不筛选
1
2
3
4
5
6
7
8
9
10
import jieba.analyse as analyse
lines = open('NBA.txt').read()
print "  ".join(analyse.extract_tags(lines, topK=20, withWeight=False, allowPOS=()))

韦少  杜兰特  全明星  全明星赛  MVP  威少  正赛  科尔  投篮  勇士  球员  斯布鲁克  更衣柜  张卫平  三连庄  NBA  西部  指导  雷霆  明星队

lines = open(u'西游记.txt').read()
print "  ".join(analyse.extract_tags(lines, topK=20, withWeight=False, allowPOS=()))

行者  八戒  师父  三藏  唐僧  大圣  沙僧  妖精  菩萨  和尚  那怪  那里  长老  呆子  徒弟  怎么  不知  老孙  国王  一个

基于 TextRank 算法的关键词抽取

  • jieba.analyse.textrank(sentence, topK=20, withWeight=False, allowPOS=(‘ns’, ‘n’, ‘vn’, ‘v’)) 直接使用，接口相同，注意默认过滤词性。

  • jieba.analyse.TextRank() 新建自定义 TextRank 实例

    算法论文： TextRank: Bringing Order into Texts

基本思想:

  • 将待抽取关键词的文本进行分词
  • 以固定窗口大小(默认为5，通过span属性调整)，词之间的共现关系，构建图
  • 计算图中节点的PageRank，注意是无向带权图

词性标注

  • jieba.posseg.POSTokenizer(tokenizer=None) 新建自定义分词器，tokenizer 参数可指定内部使用的 jieba.Tokenizer 分词器。jieba.posseg.dt 为默认词性标注分词器。
  • 标注句子分词后每个词的词性，采用和 ictclas 兼容的标记法。
  • 具体的词性对照表参见计算所汉语词性标记集
1
2
3
4
5
6
7
8
9
import jieba.posseg as pseg
words = pseg.cut("我爱自然语言处理")
for word, flag in words:
    print('%s %s' % (word, flag))
    
我 r
爱 v
自然语言 l
处理 v

并行分词

原理：将目标文本按行分隔后，把各行文本分配到多个 Python 进程并行分词，然后归并结果，从而获得分词速度的可观提升 基于 python 自带的 multiprocessing 模块，目前暂不支持 Windows 

1
2
jieba.enable_parallel(4) # 开启并行分词模式，参数为并行进程数
jieba.disable_parallel() # 关闭并行分词模式

Word2Vec

Word2vec，把词映射为实数域向量的技术也叫词嵌入（word embedding）,不使用onehot编码

两个生成词汇向量的算法

两套效率中等的训练算法

Skip-gram

由于onthot编码的向量相互正交，无法通过内积进行相似度计算，因此将onthot编码的词向量转换为d维的向量。

方法是用监督学习（窗口内的背景词作为监督信息）进行训练，最后只取隐层信息（fake task），也就是权重矩阵作为映射后的向量表达。为了将onthot编码映射到d维（假设d=300），那么想到的方法是矩阵运算，由于一个单词的onthot编码大小是n维（n为单词数），为了映射到300维，需要一个n*300大小的矩阵。

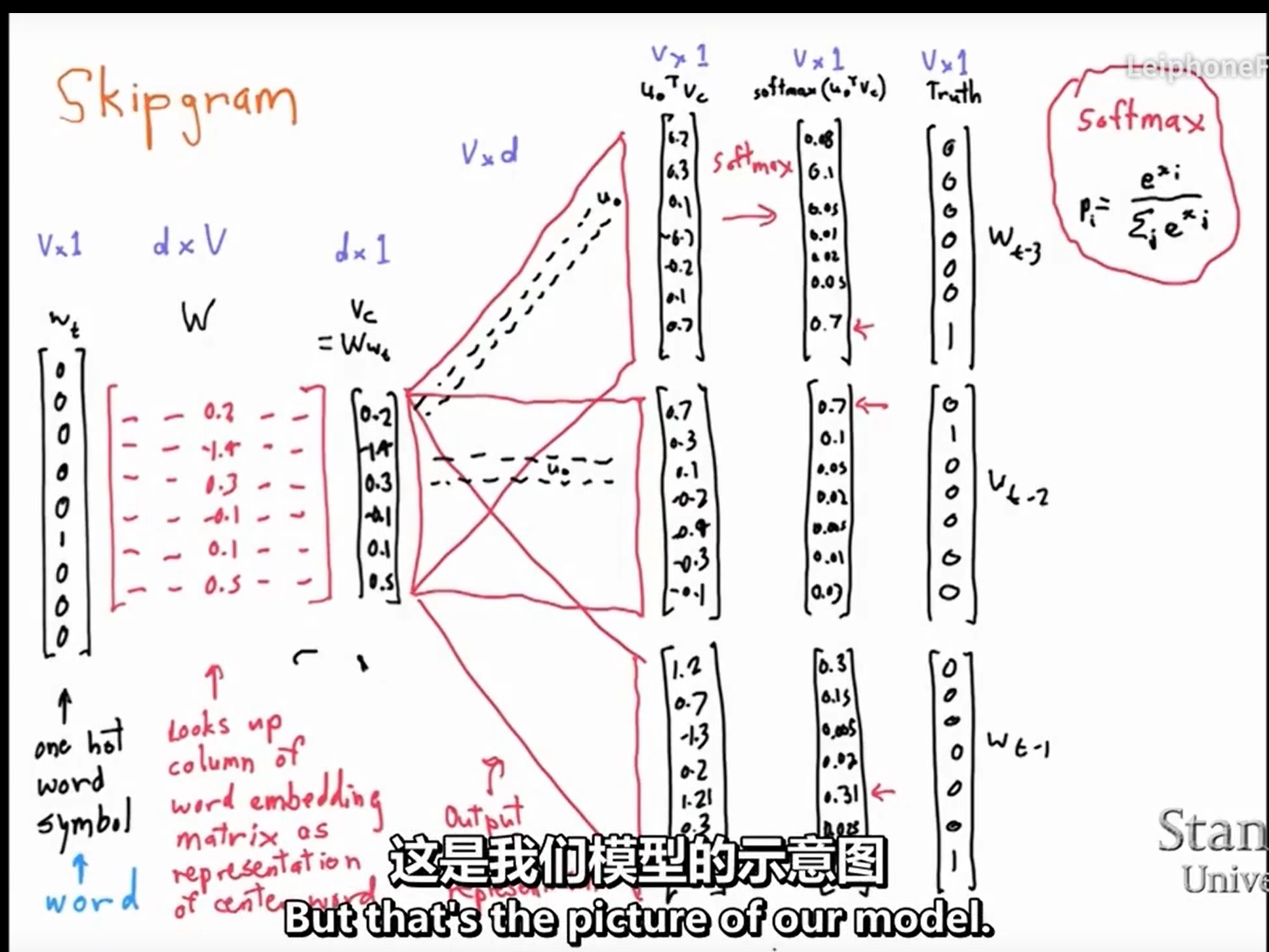
对于输入的一个词（onehot）和权重矩阵相乘，取其对应的列（lookup）,得到稠密的向量表示。第一个权重矩阵为中心词矩阵，第二个为上下文矩阵，一个词有两种向量表达（可能作为中心词，也可能作为上下文）。矩阵随机初始化

训练样本是（input word, output word ) 这样的单词对，如（dirve, car）,这种单词对从窗口里面取

这一个红框就代表一个样本，这三个红框其实是用三个样本训练了三次

和所有单词做内积（近似为相似度），通过监督学习进行训练

https://blog.csdn.net/weixin_41843918/article/details/90312339

n-gram

如果有一个由 m 个词组成的序列（或者说一个句子），我们希望算得概率 [公式] ，根据链式规则，可得

[公式]

这个概率显然并不好算，不妨利用马尔科夫链的假设，即当前这个词仅仅跟前面几个有限的词相关，因此也就不必追溯到最开始的那个词，这样便可以大幅缩减上述算式的长度。即

[公式]

这个马尔科夫链的假设为什么好用？我想可能是在现实情况中，大家通过真实情况将n=1，2，3，….这些值都试过之后，得到的真实的效果和时间空间的开销权衡之后，发现能够使用

下面给出一元模型，二元模型，三元模型的定义：

当 n=1, 一个一元模型（unigram model)即为 ：

img

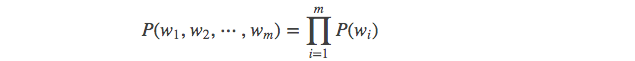
当 n=2, 一个二元模型（bigram model)即为 ：

img

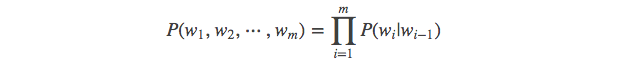
当 n=3, 一个三元模型（trigram model)即为

img

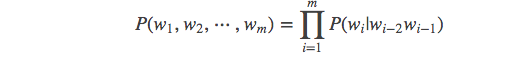
然后下面的思路就很简单了，在给定的训练语料中，利用贝叶斯定理，将上述的条件概率值（因为一个句子出现的概率都转变为右边条件概率值相乘了）都统计计算出来即可。下面会给出具体例子讲解。这里先给出公式：

img

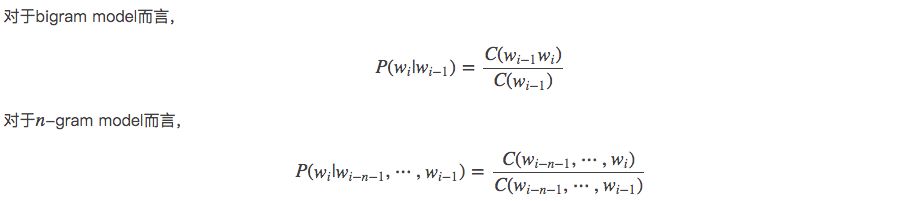
对第一个进行解释，后面同理,如下： [公式]

下面给出具体的例子。

下面例子来自于：自然语言处理中的N-Gram模型详解 - 白马负金羁 - CSDN博客和《北京大学 常宝宝 以及 The University of Melbourne “Web Search and Text Analysis” 课程的幻灯片素材》

假设现在有一个语料库，我们统计了下面的一些词出现的数量

img

下面的这些概率值作为已知条件：

img

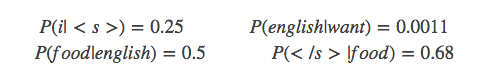
p(want|< s>) = 0.25​

下面这个表给出的是基于Bigram模型进行计数之结果

img

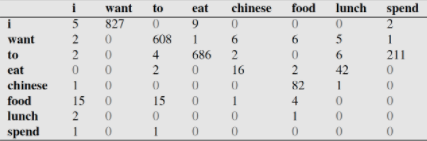
例如，其中第一行，第二列 表示给定前一个词是 $i$时，当前词为$want$的情况一共出现了827次。据此，我们便可以算得相应的频率分布表如下。

img

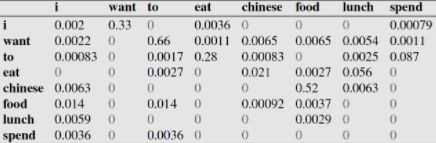
比如说，我们就以表中的$p(eat|i)=0.0036$这个概率值讲解，从表一得出$i$一共出现了2533次，而其后出现$eat$的次数一共有9次，$p(eat|i)=p(eat,i)/p(i)=count(i,eat)/count(i)=9/2533 = 0.0036$

下面我们通过基于这个语料库来判断s1= < s> i want english food< /s> ​与​s2 = < s> want i english food< /s>​哪个句子更合理：

首先判断p(s1)

再求p(s2)？

通过比较我们可以明显发现$0.00000002057<0.000031$,也就是说s1= i want english food更像人话。

再深层次的分析，我们可以看到这两个句子的概率的不同，主要是由于顺序i want还是want i的问题，根据我们的直觉和常用搭配语法，i want要比want i出现的几率要大很多。所以两者的差异，第一个概率大，第二个概率小，也就能说的通了。

Beam Search

Beam search（集束）和Greedy search（贪心）解码常用的算法。

在机器翻译中，beam search算法在测试的时候用的，因为在训练过程中，每一个decoder的输出是有与之对应的正确答案做参照，也就不需要beam search去加大输出的准确率。

以中翻英作为例子：

1
2
我 爱 学习，学习 使 我 快乐
I love learning, learning makes me happy

记中文序列为$X$，首先使用seq2seq中的encoder对中文序列进行编码，得到语义向量$C$

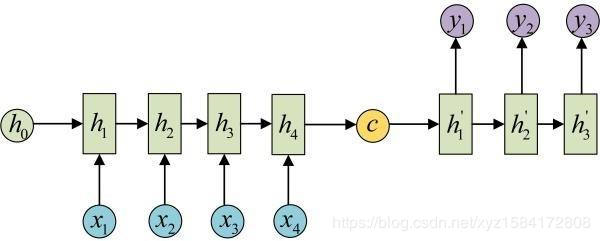
seq2seq

之后decoder对语义向量$C$进行解码，翻译成目标语言。解码之前需要设置beam size，为k个最有可能的结果。此处设置为3.

来看解码器的第一个输出$y_1$，在给定语义向量$C$的情况下，首先选择英语词汇表中最有可能k个单词，也就是依次选择条件概率$P(y_1∣C)$前3大对应的单词，比如这里概率最大的前三个单词依次是：$I，learning，happy$

接着生成第二个输出$y_2$，在这个时候我们得到了那些东西呢，首先我们得到了编码阶段的语义向量$C$，还有第一个输出$y_1$。此时有个问题，$y_1$有三个，怎么作为这一时刻的输入呢（解码阶段需要将前一时刻的输出作为当前时刻的输入），答案就是都试下，具体做法是：

  • 确定$I$为第一时刻的输出，将其作为第二时刻的输入，得到在已知$(C, I)$的条件下，各个单词作为该时刻输出的条件概率$P(y_2|C,I)$，有6个组合，每个组合的概率为$P(I|C)P(y_2|C, I)$。
  • 确定$leanring$为第一时刻的输出，将其作为第二时刻的输入，得到该条件下，词汇表中各个单词作为该时刻输出的条件概率$P(y_2|C, learning)$，这里同样有6种组合；
  • 确定$happy$为第一时刻的输出，将其作为第二时刻的输入，得到该条件下各个单词作为输出的条件概率$P(y_2|C, happy)$，得到6种组合，概率的计算方式和前面一样。

这样就得到了18个组合，每一种组合对应一个概率值$P(y_1|C)P(y_2|C, y_1)$，接着在这18个组合中选择概率值top3的那三种组合，假设得到$Ilove,Ihappy,leanring make$。
接下来要做的重复这个过程，逐步生成单词，直到遇到结束标识符停止。最后得到概率最大的那个生成序列。其概率为：

以上就是Beam search算法的思想，当beam size=1时，就变成了贪心算法。