目标检测一
非极大值抑制nms
nms
目标检测算法会产生数量巨大的候选矩形框,这些矩形框有很多是指向同一目标,存在大量冗余。nms可以消除多余的框,找到最佳的物体检测位置。
非极大值抑制(Non-Maximum Suppression)的思想是搜索局部极大值,抑制非极大值元素
交并比
IoU(Intersection over Union)为交并比 。
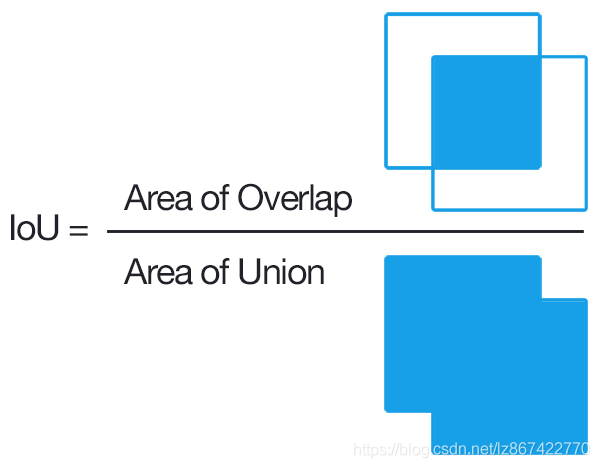
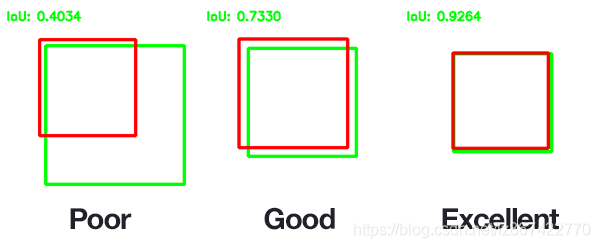
经典nms
- 设定目标框的置信度阈值,常用的阈值是0.5左右
- 根据置信度降序排列候选框列表
- 选取置信度最高的框A添加到输出列表,并将其从候选框列表中删除
- 计算A与候选框列表中的所有框的IoU值,删除大于阈值的候选框
- 重复上述过程,直到候选框列表为空,返回输出列表
soft-NMS
经典NMS对于重叠物体无法很好检测。
下图中红色边界框的置信度最高,绿色框的置信度较小,但和红色框的IoU较大,如果按NMS规则,那么此时绿色框的置信度则置为0。可是实际上,绿色框是后面那匹马的边界框,而红色框是前面那匹马的边界框,两者应该同时存在。
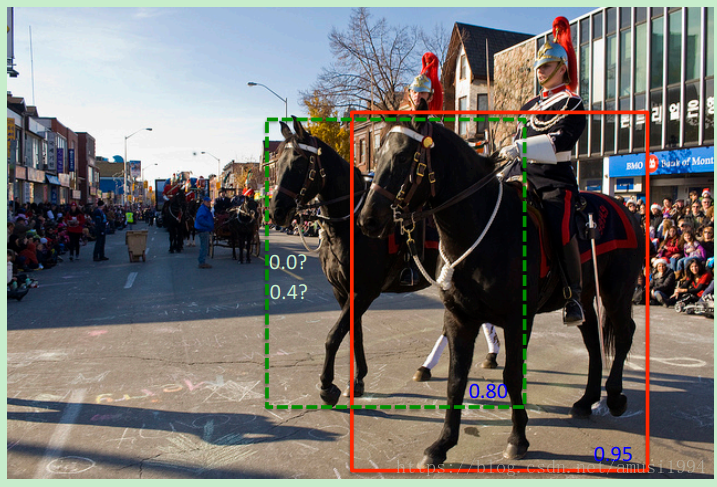
相对于经典NMS算法,Soft-NMS仅仅修改了一行代码。当选取了最大置信度的Bounding box之后,计算其余每个Bounding box与Bounding box的Iou值,经典NMS算法的做法是直接删除Iou大于阈值的Bounding box;而Soft-NMS则是使用一个基于Iou的衰减函数,降低Iou大于阈值Nt的Bounding box的置信度,IoU越大,衰减程度越大。
经典NMS
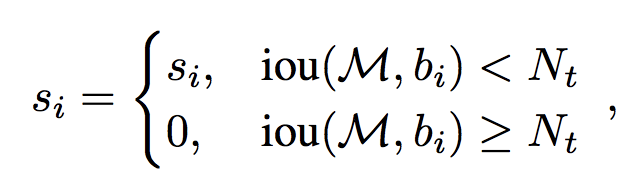
soft-NMS-线性
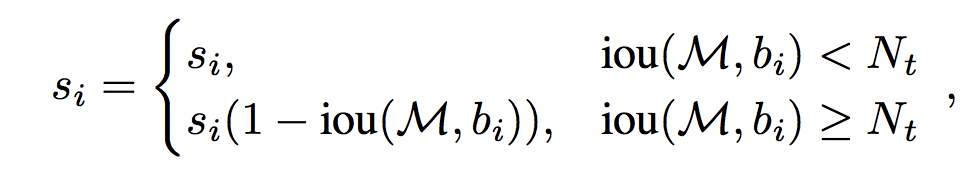
soft-NMS-高斯
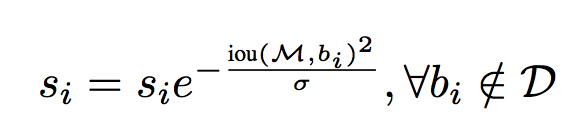
Locality-Aware NMS
假设来自附近像素的几何图形往往高度相关,我们建议逐行合并几何图形,同时在同一行中合并几何图形时,我们将迭代地合并当前遇到的几何图形和最后合并的几何图形。这种改进的技术在最佳场景下以$O(n)$运行。即使最坏的情况也与经典NMS相同,只要位置假设成立,算法在实践中运行得足够快。

1 | import numpy as np |
softer-NMS
以上的NMS算法,无论是经典NMS还是Soft-NMS算法,都是在一种假设前提下:置信度最高的Bounding box就是目标的候选位置最精确的物体位置。但是事实上,这个假设可能并不成立,或者说并不那么精确。针对这个问题,来自卡内基梅隆大学与旷视科技的研究人员在文中提出了一种新的非极大抑制算法Softer-NMS,显著改进了目标检测的定位精度。
论文的motivation来自于NMS时用到的score仅仅是分类置信度得分,不能反映Bounding box的定位精准度,既分类置信度和定位置信非正相关的 ,
论文首先假设Bounding box是高斯分布,ground truth bounding box是狄拉克delta分布(即标准方差为0的高斯分布极限)。KL 散度用来衡量两个概率分布的非对称性度量,KL散度越接近0代表两个概率分布越相似。
论文提出的KL loss,即为最小化Bounding box regression loss,既Bounding box的高斯分布和ground truth的狄拉克delta分布的KL散度。直观上解释,KL Loss使得Bounding box预测呈高斯分布,且与ground truth相近。而将包围框预测的标准差看作置信度。
论文提出的Softer-NMS,基于soft-NMS,对预测标注方差范围内的候选框加权平均,使得高定位置信度的bounding box具有较高的分类置信度。
Softer-NMS网络结构,与R-CNN不同的是引入absolute value layer(图中AbsVal),实现标注方差的预测:
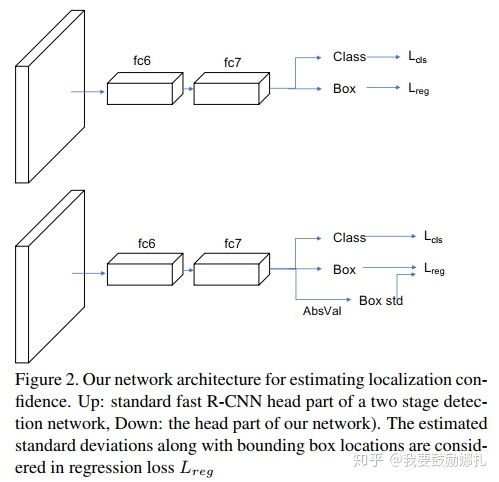

预测的四个顶点坐标,分别对$IoU>Nt$的预测加权平均计算,得到新的4个坐标点。第i个box的x1计算公式如下(j表示所有$IoU>Nt$的box) :
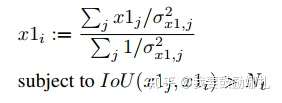

Selective Search
1 | 可以通过pip安装selectivesearch |
首先通过简单的区域划分算法,将图片划分成很多小区域,再通过相似度和区域大小(小的区域先聚合,这样是防止大的区域不断的聚合小区域,导致层次关系不完全)不断的聚合相邻小区域,类似于聚类的思路。这样就能解决object层次问题。

step0:生成区域集R,具体参见论文《Efficient Graph-Based Image Segmentation》
step1:计算区域集R里每个相邻区域的相似度S={s1,s2,…}
step2:找出相似度最高的两个区域,将其合并为新集,添加进R
step3:从S中移除所有与step2中有关的子集
step4:计算新集与所有子集的相似度
step5:跳至step2,直至S为空
为了保证能够划分的完全,对于相似度,作者提出了可以多样化的思路,不但使用多样的颜色空间(RGB,Lab,HSV等等),还有很多不同的相似度计算方法
通过上述的步骤我们能够得到很多很多的区域,但是显然不是每个区域作为目标的可能性都是相同的,因此我们需要衡量这个可能性,这样就可以根据我们的需要筛选区域建议个数啦。
这篇文章做法是,给予最先合并的图片块较大的权重,比如最后一块完整图像权重为1,倒数第二次合并的区域权重为2以此类推。但是当我们策略很多,多样性很多的时候呢,这个权重就会有太多的重合了,排序不好搞啊。文章做法是给他们乘以一个随机数,毕竟3分看运气嘛,然后对于相同的区域多次出现的也叠加下权重,毕竟多个方法都说你是目标,也是有理由的嘛。这样我就得到了所有区域的目标分数,也就可以根据自己的需要选择需要多少个区域了。
1 | # 从https://github.com/AlpacaDB/selectivesearch下载示例代码,运行example.py |
