一、机器学习介绍&线性、逻辑回归
什么是机器学习
- 要学什么—决策函数
- 从哪里学—训练数据
- 怎样学习—求解机器学习模型
针对某个任务 (Task ),利用训练数据 (Experience ),求
解一个学习模型,从而提高该任务的性能 (Performance)
机器学习要素:
- 任务、目标(Task)
- 使用经验数据(Experience)
- 提高学习性能(Performance)
线性、逻辑回归
多元线性回归
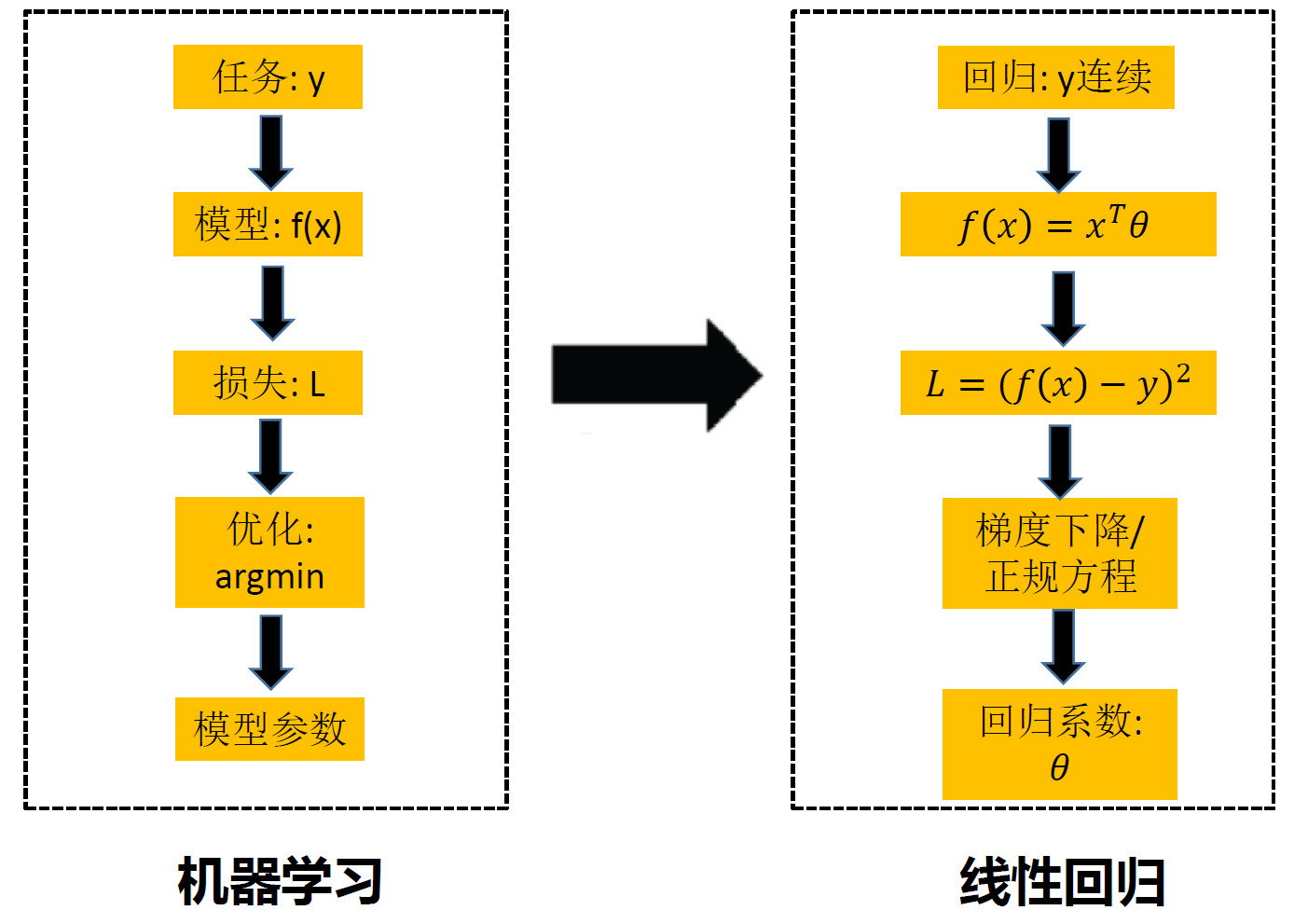

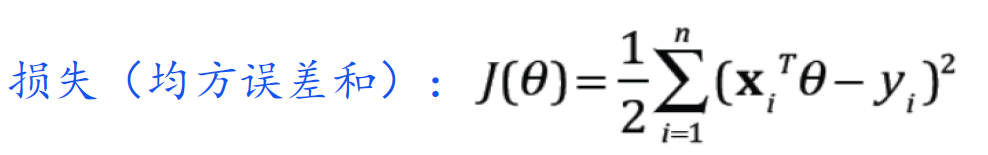
损失函数几何意义:试图找到一个超平面,使所有样本到超平面上的欧式距离之和最小
梯度下降法求解
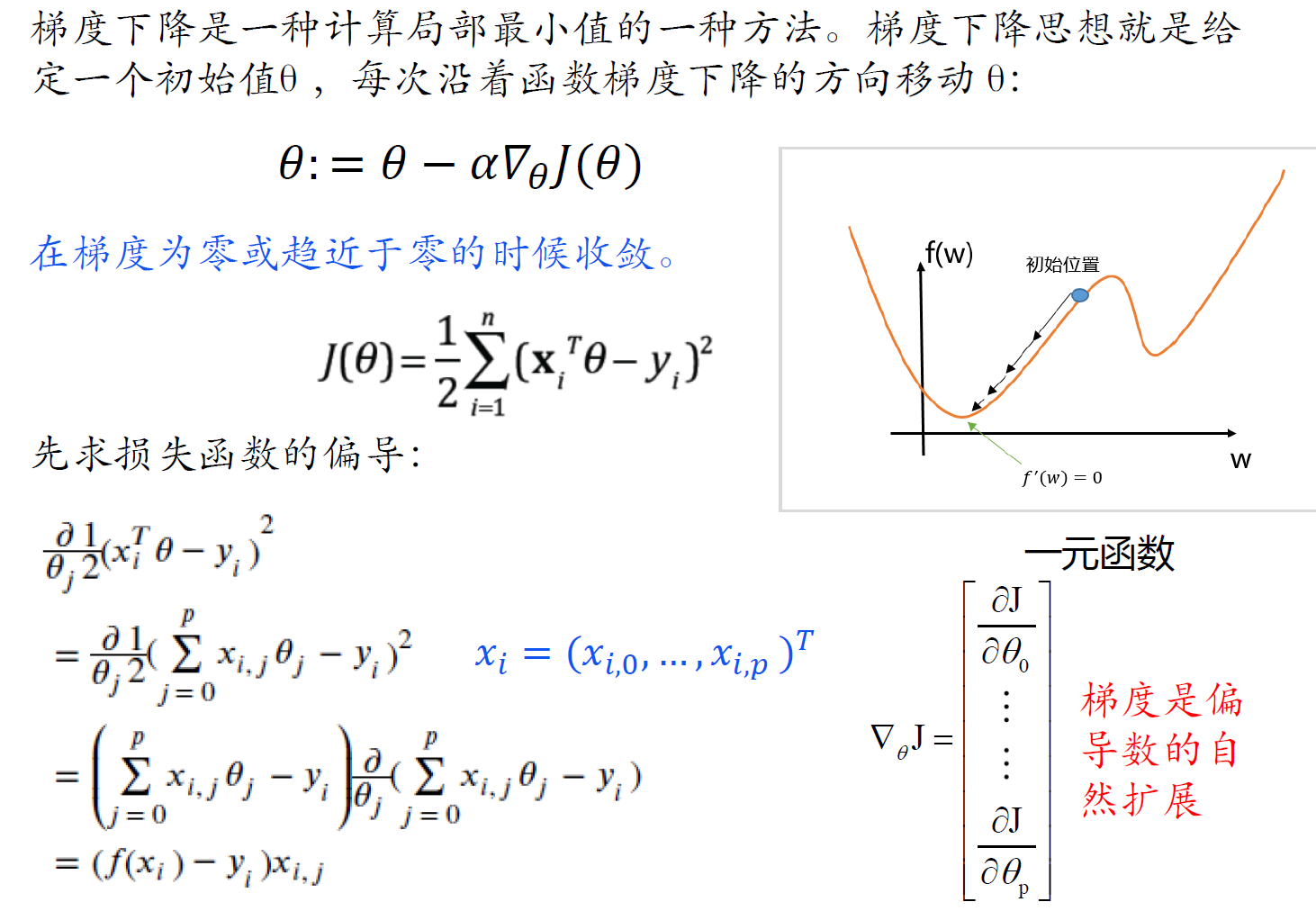

随机梯度下降法

正规方程



比较

- MSE (mean square error) 均方误差
F1 measure
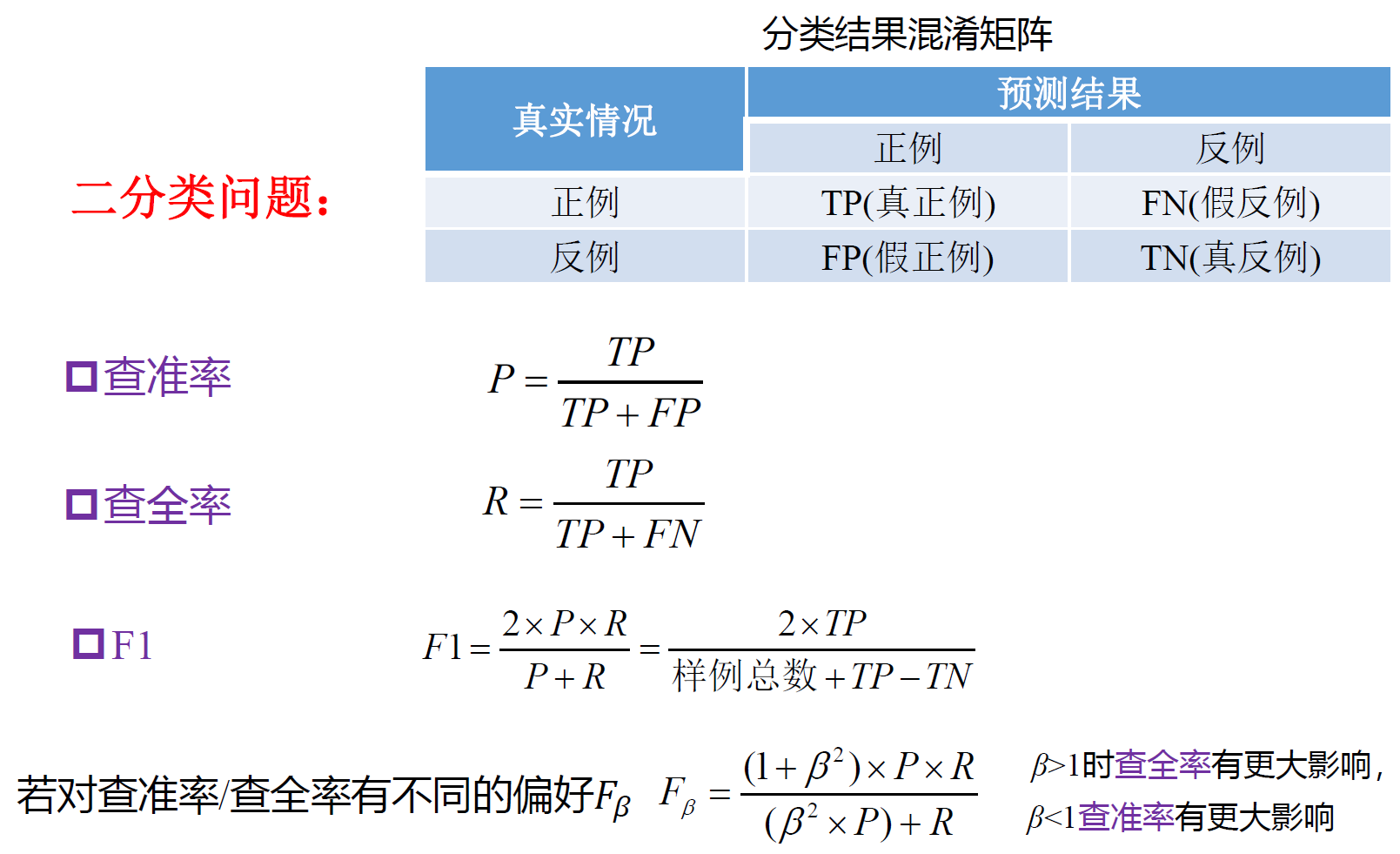
逻辑回归


梯度上升法求解:
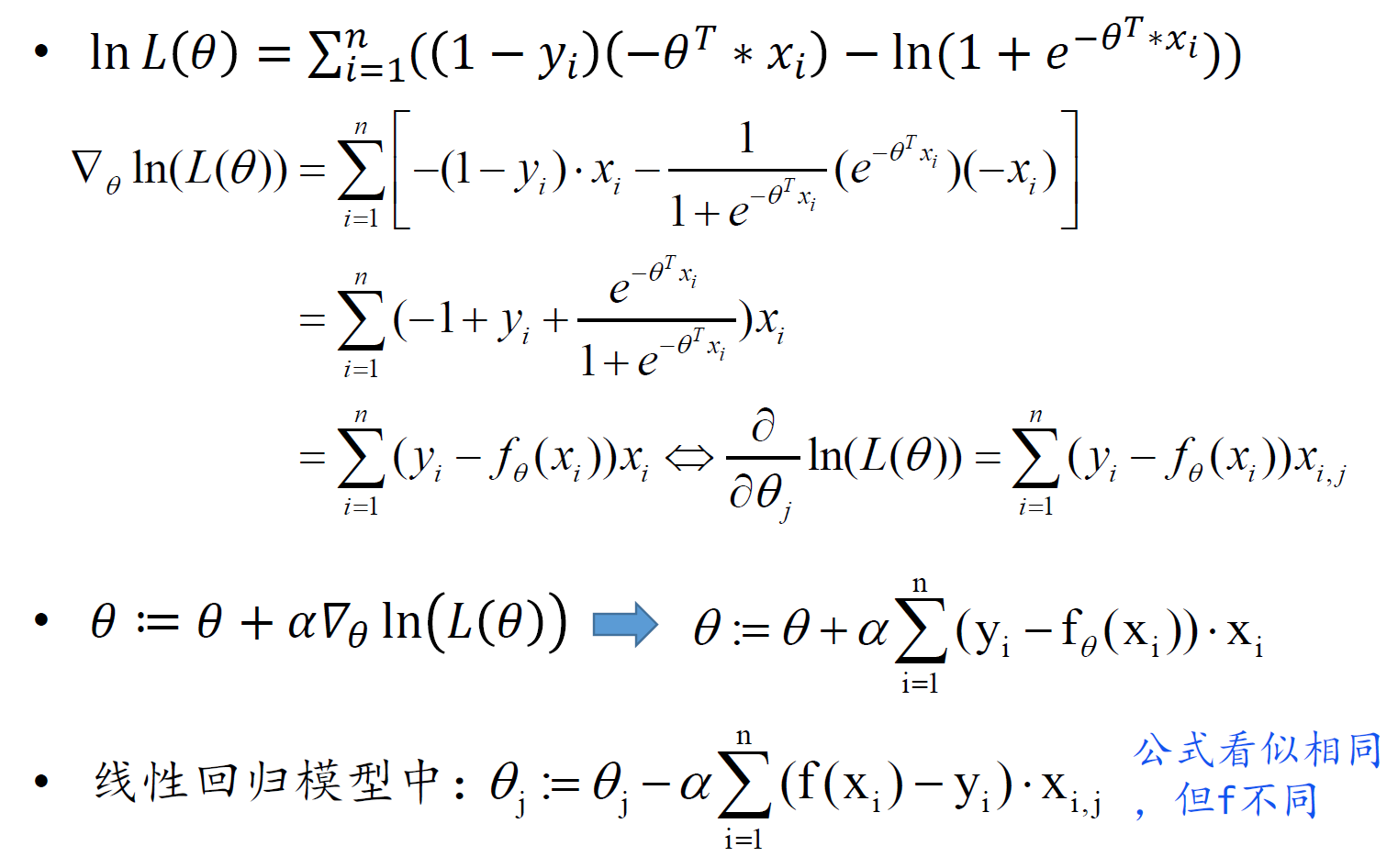
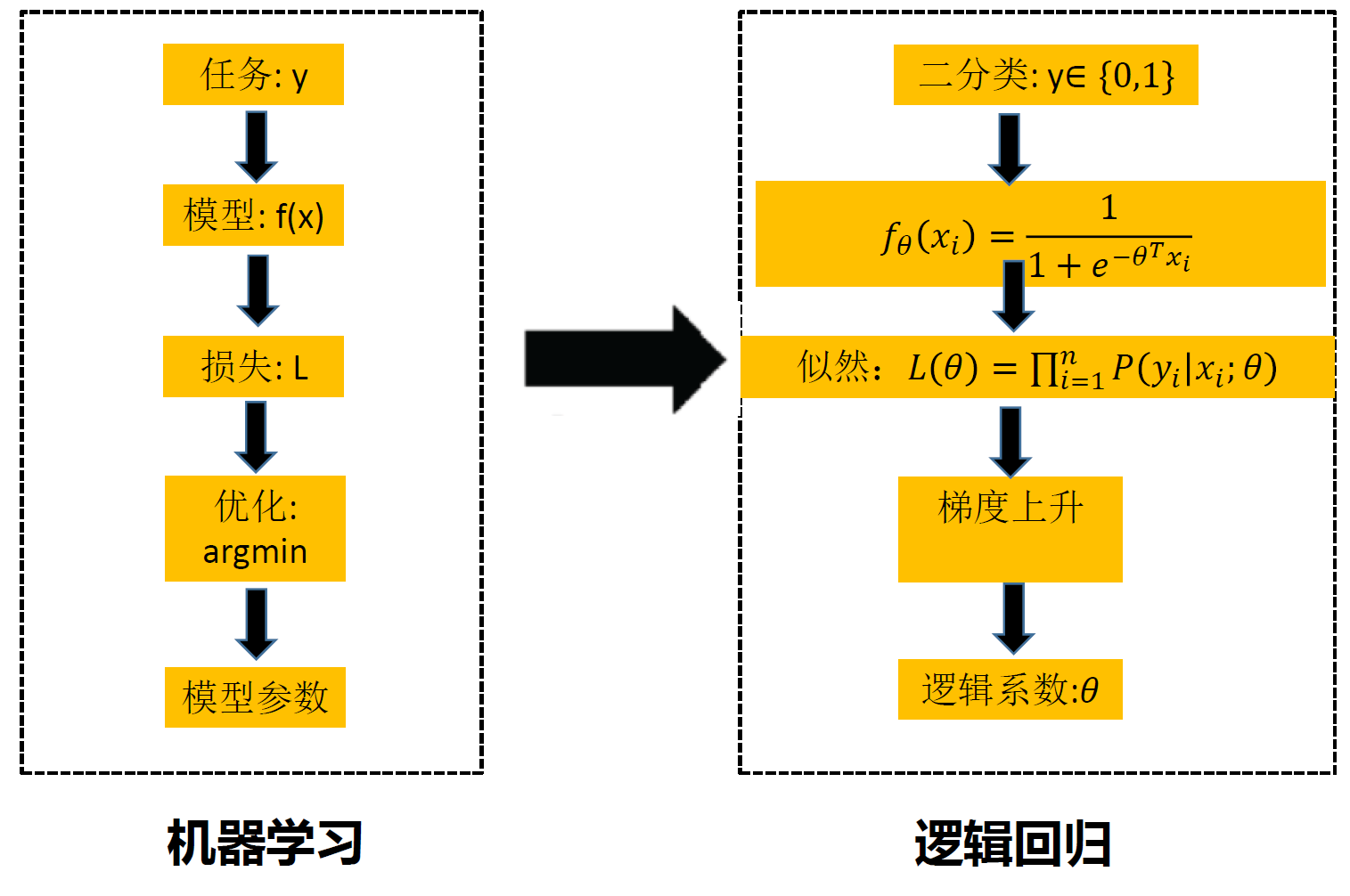
二、神经网络
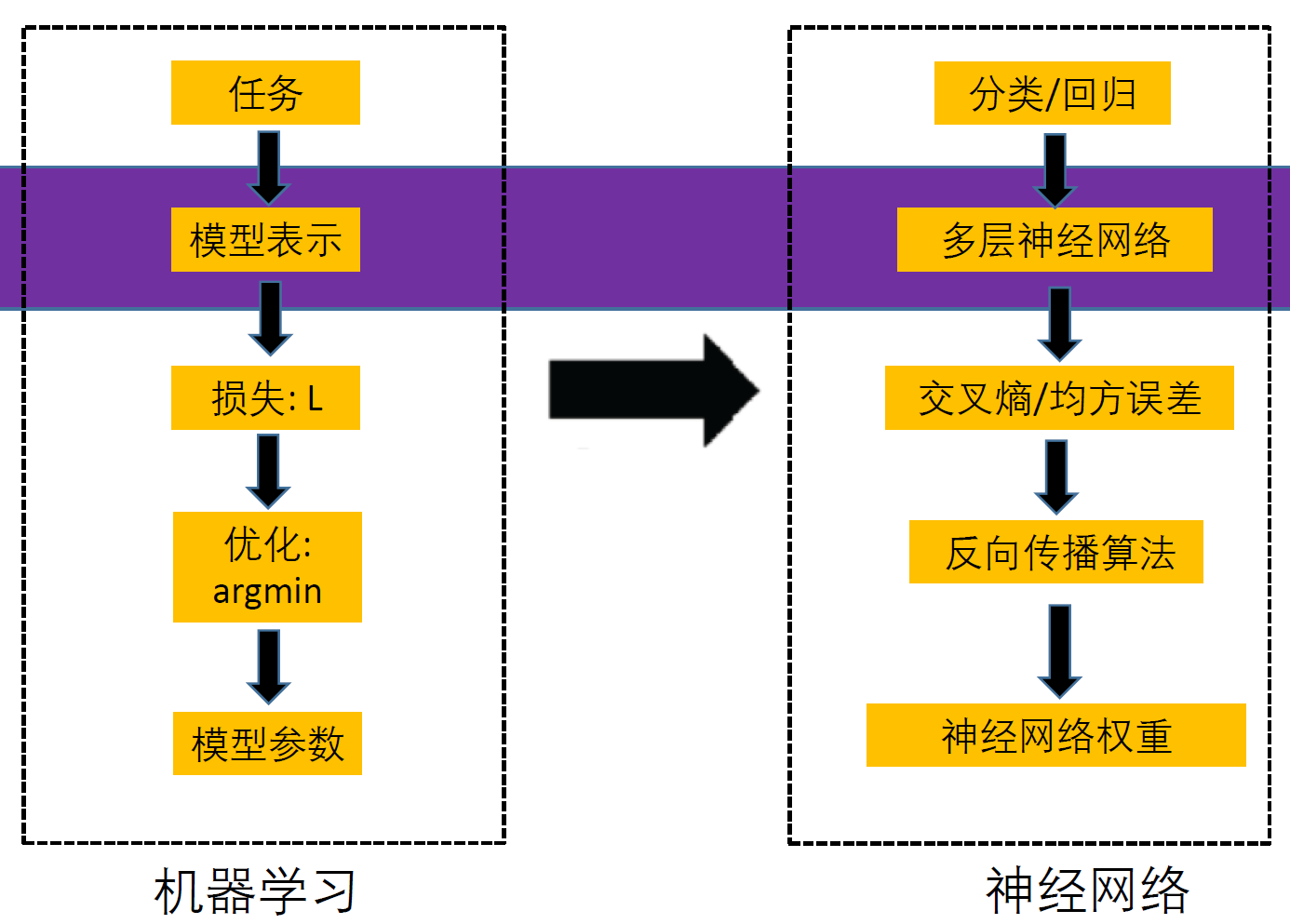
损失
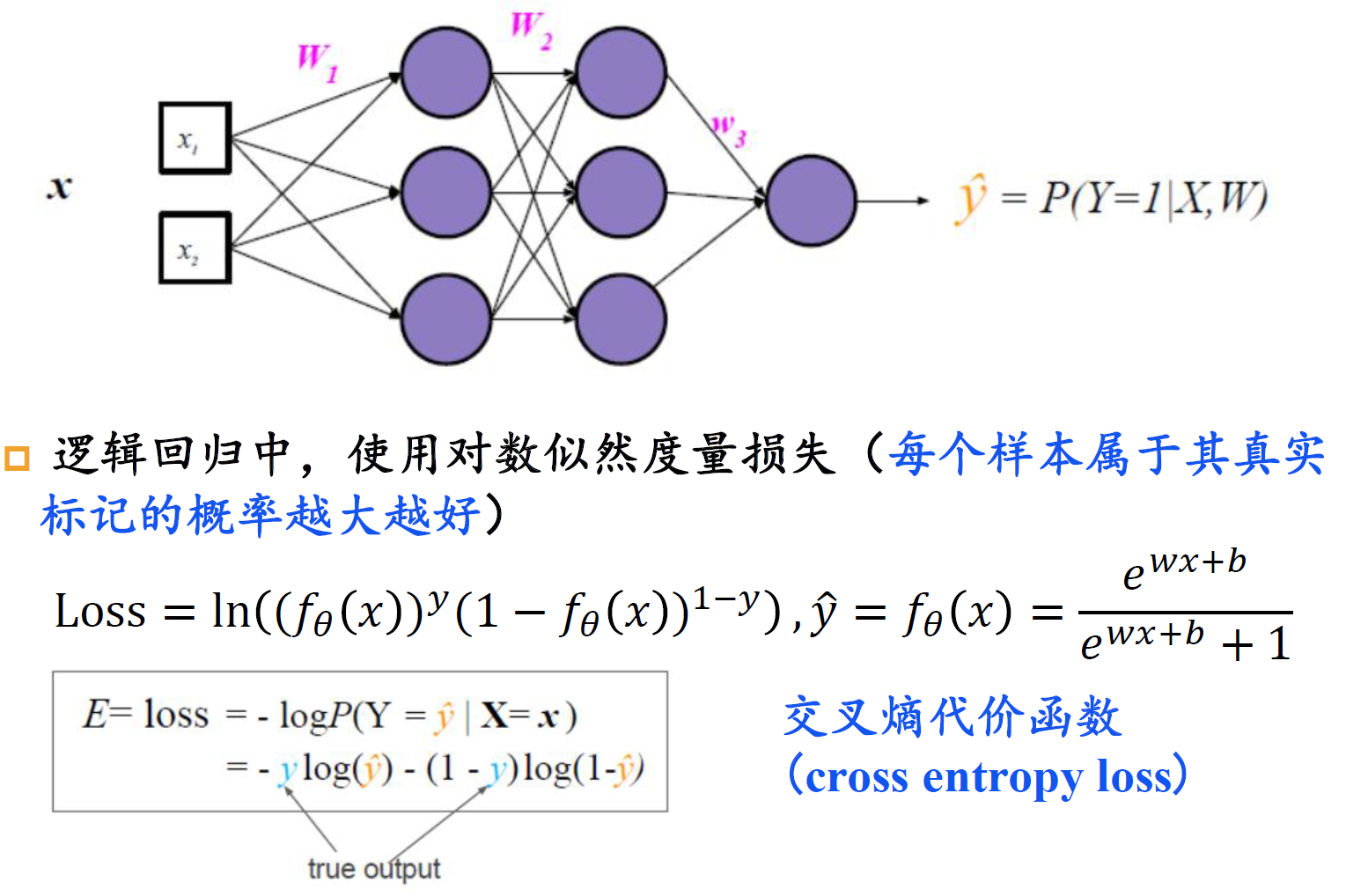
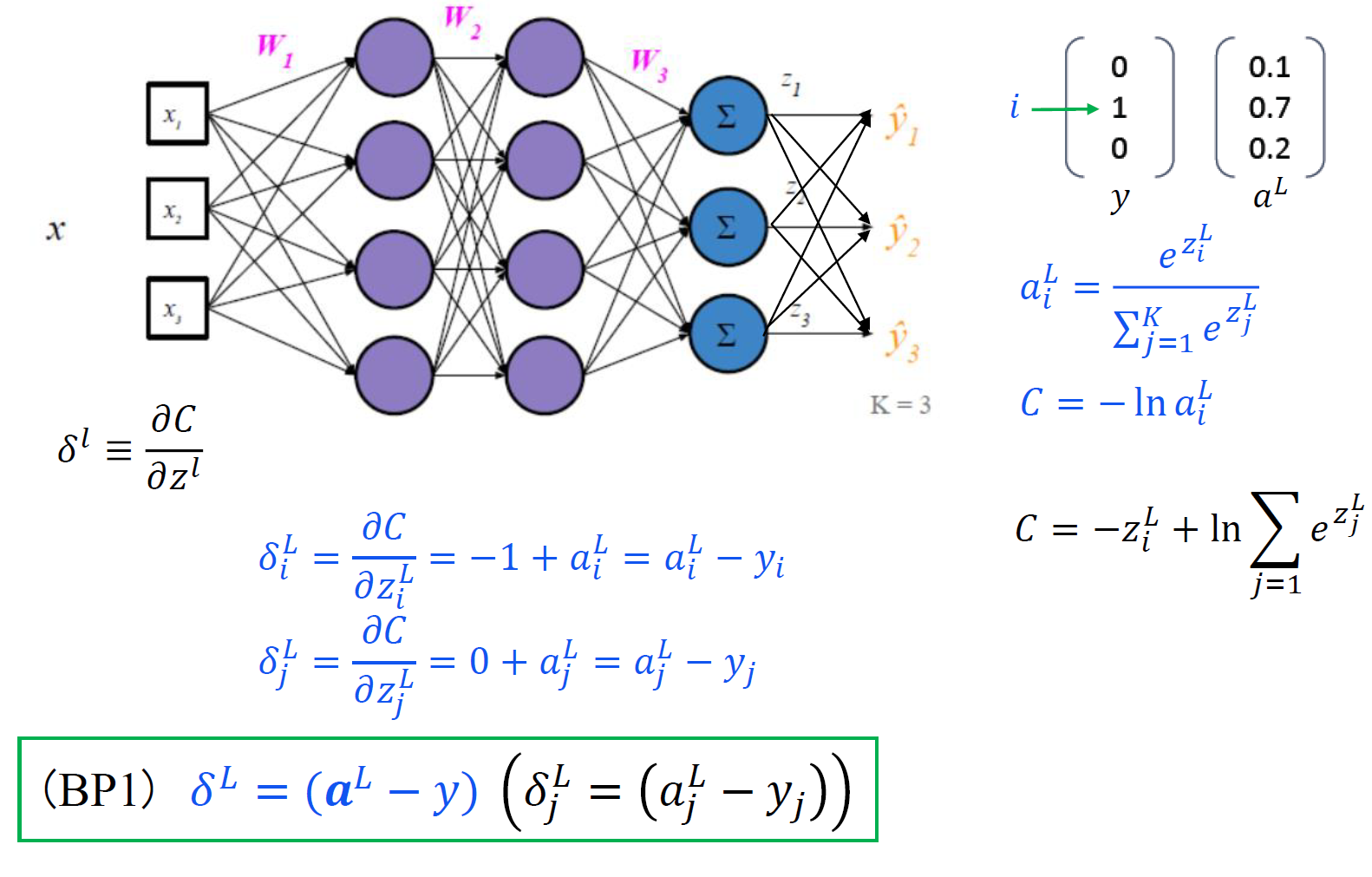
二分类损失
多分类损失
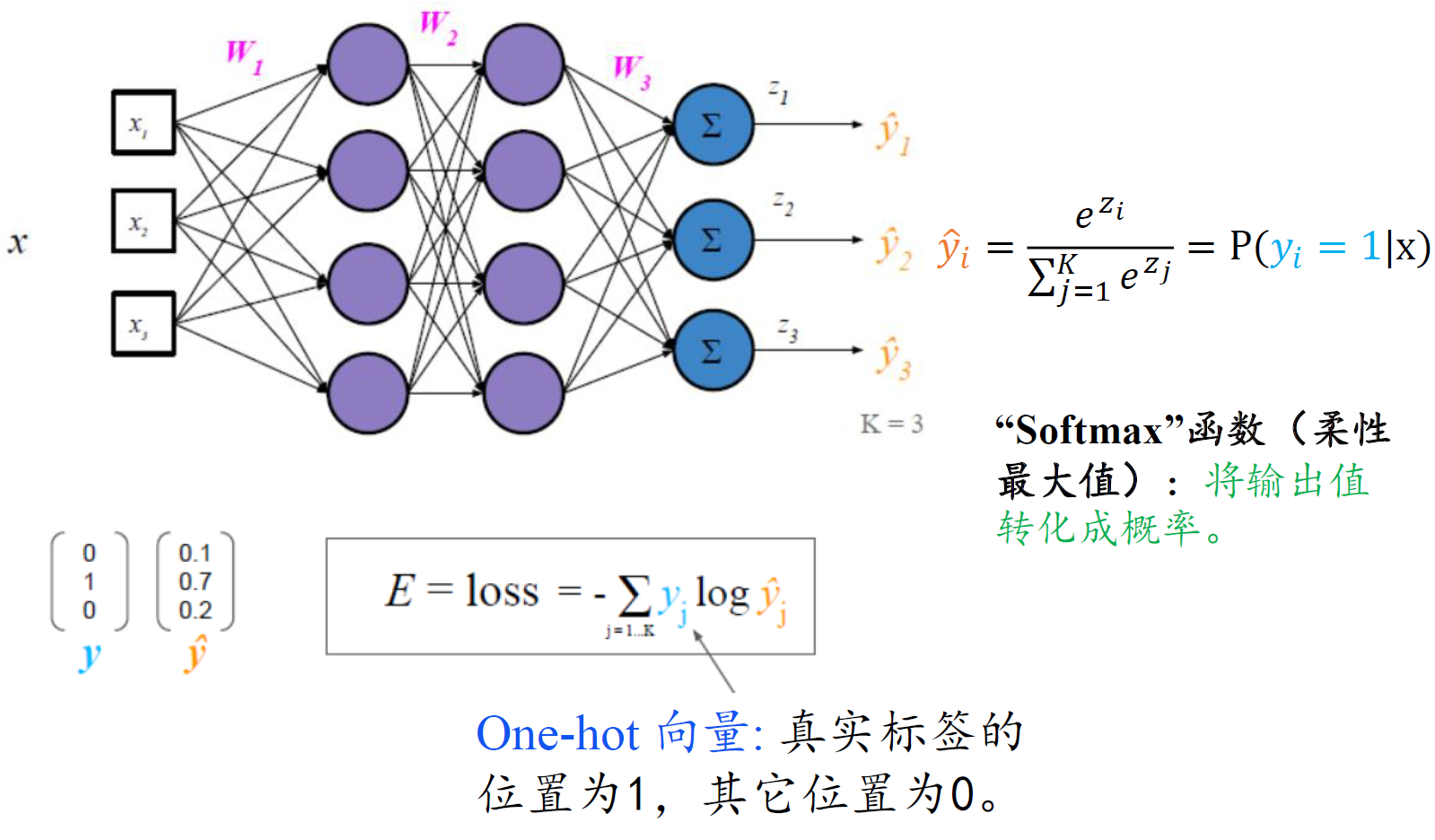
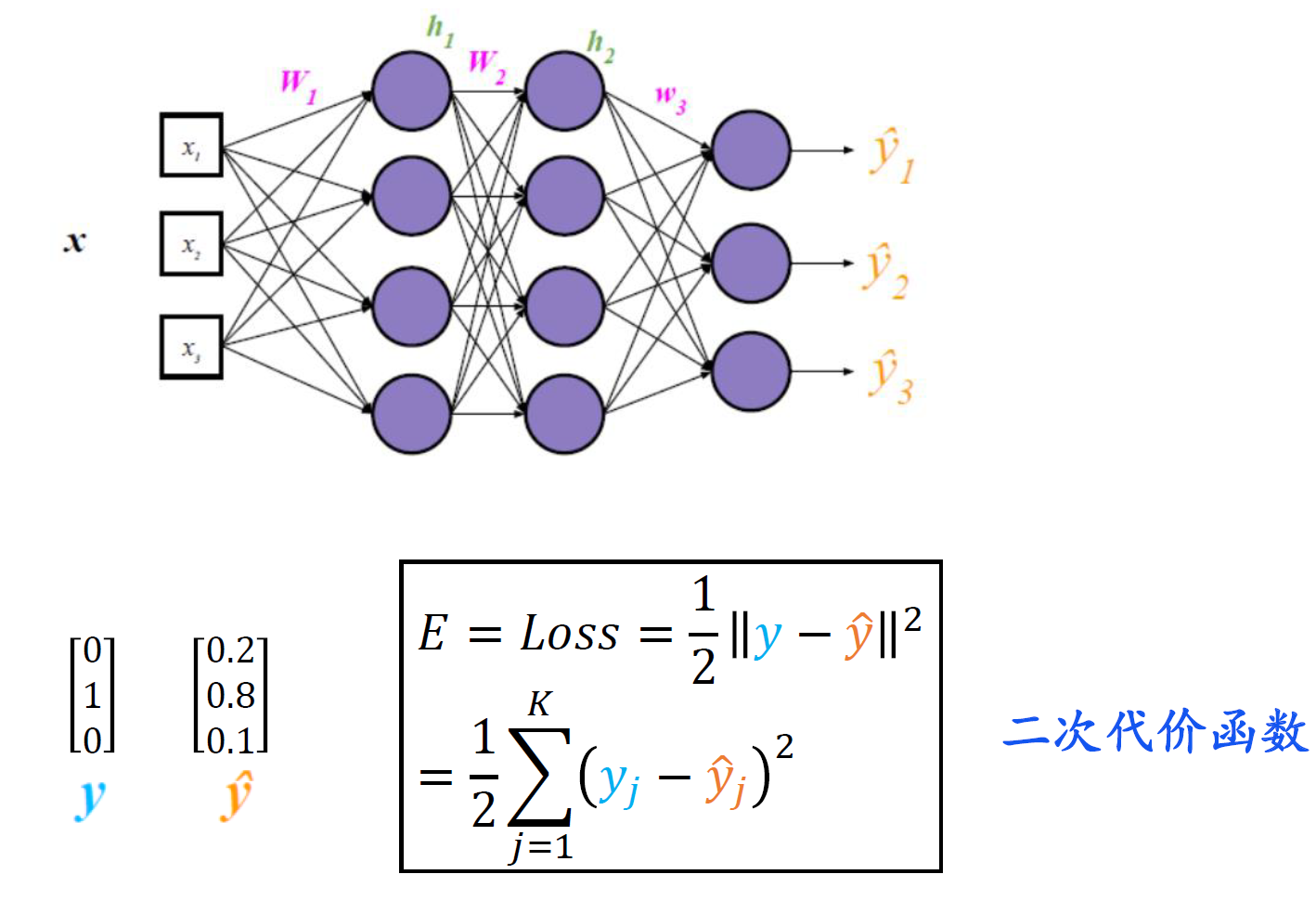
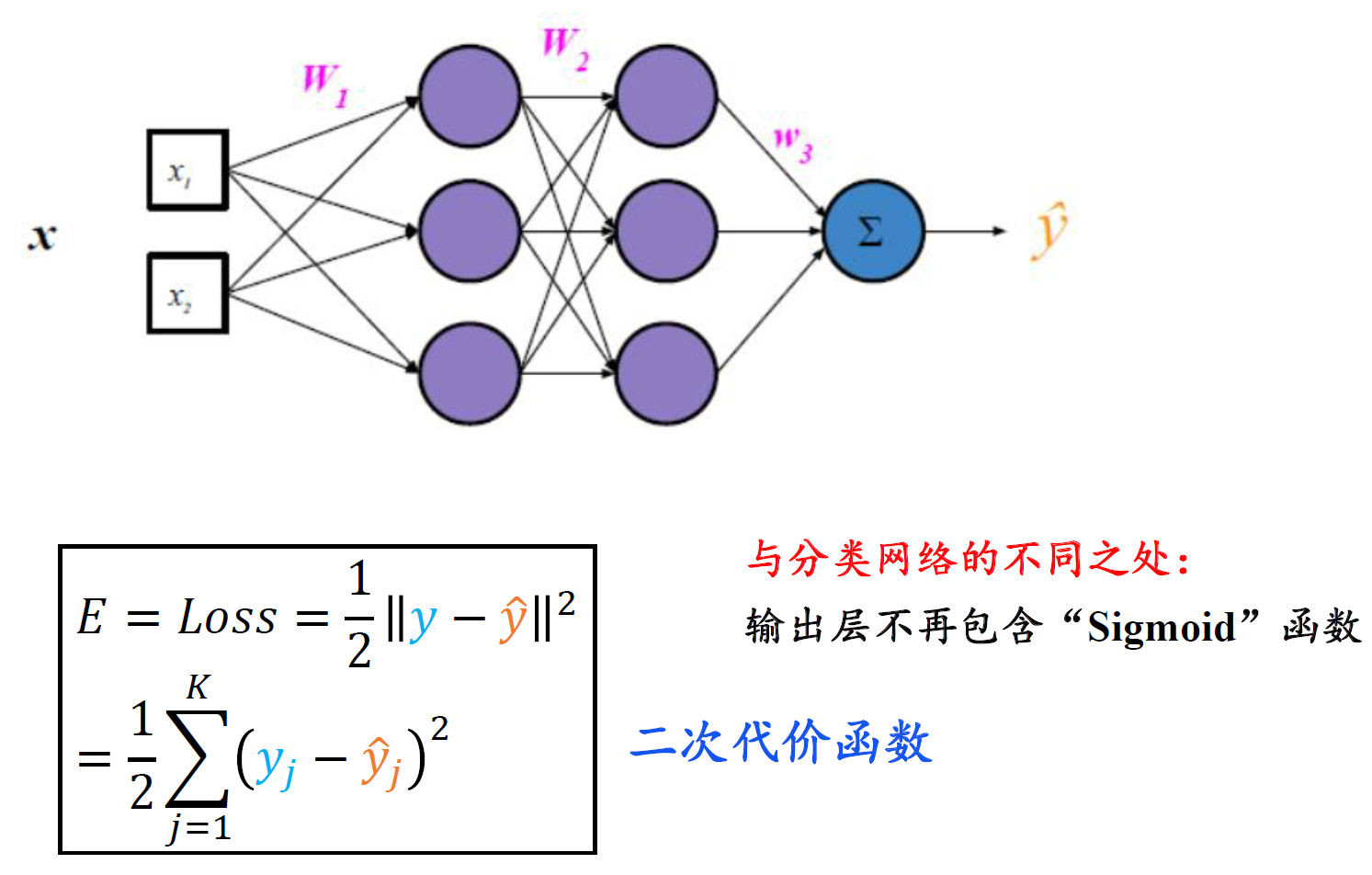
回归损失
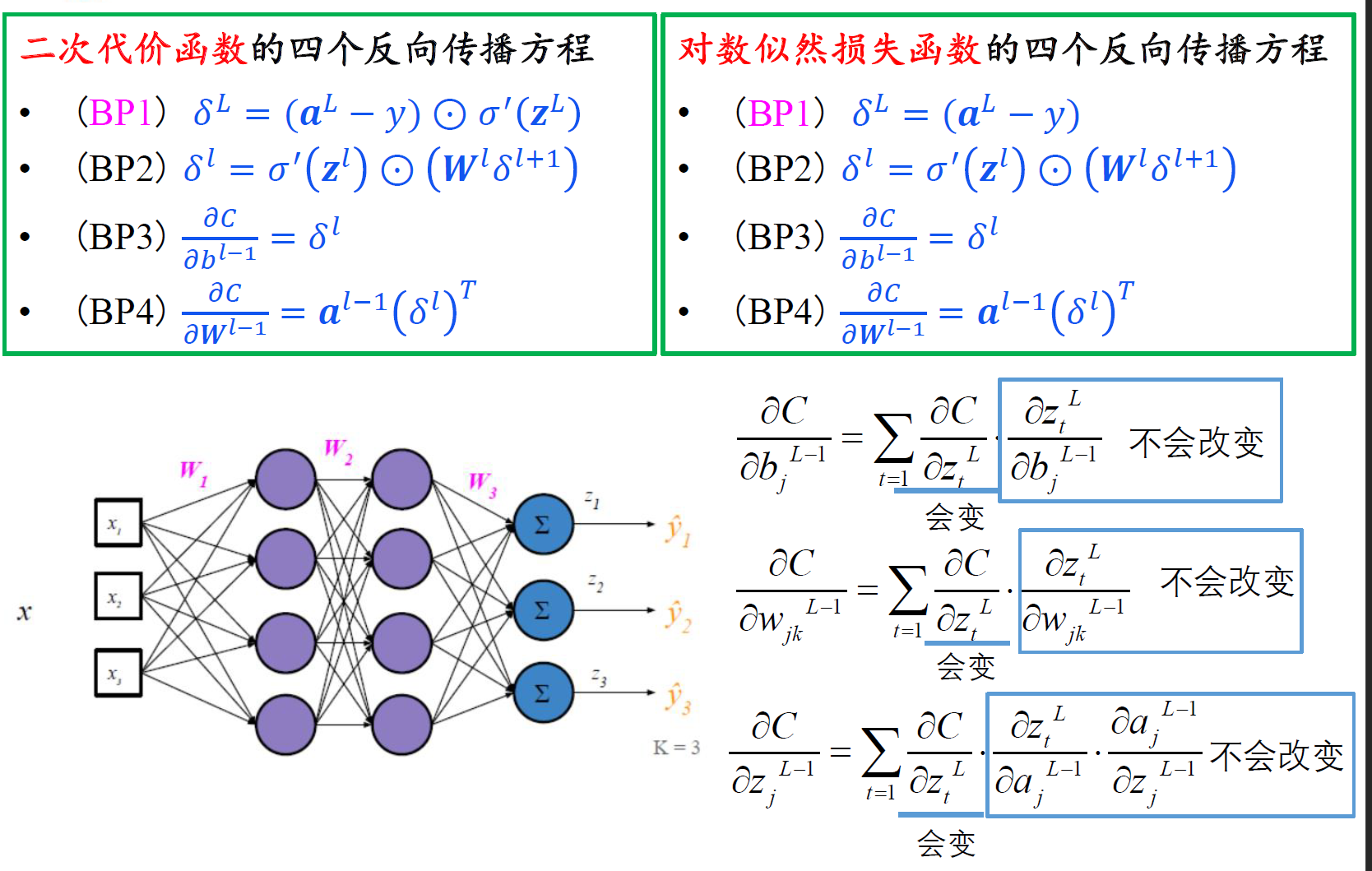
反向传播一般情形
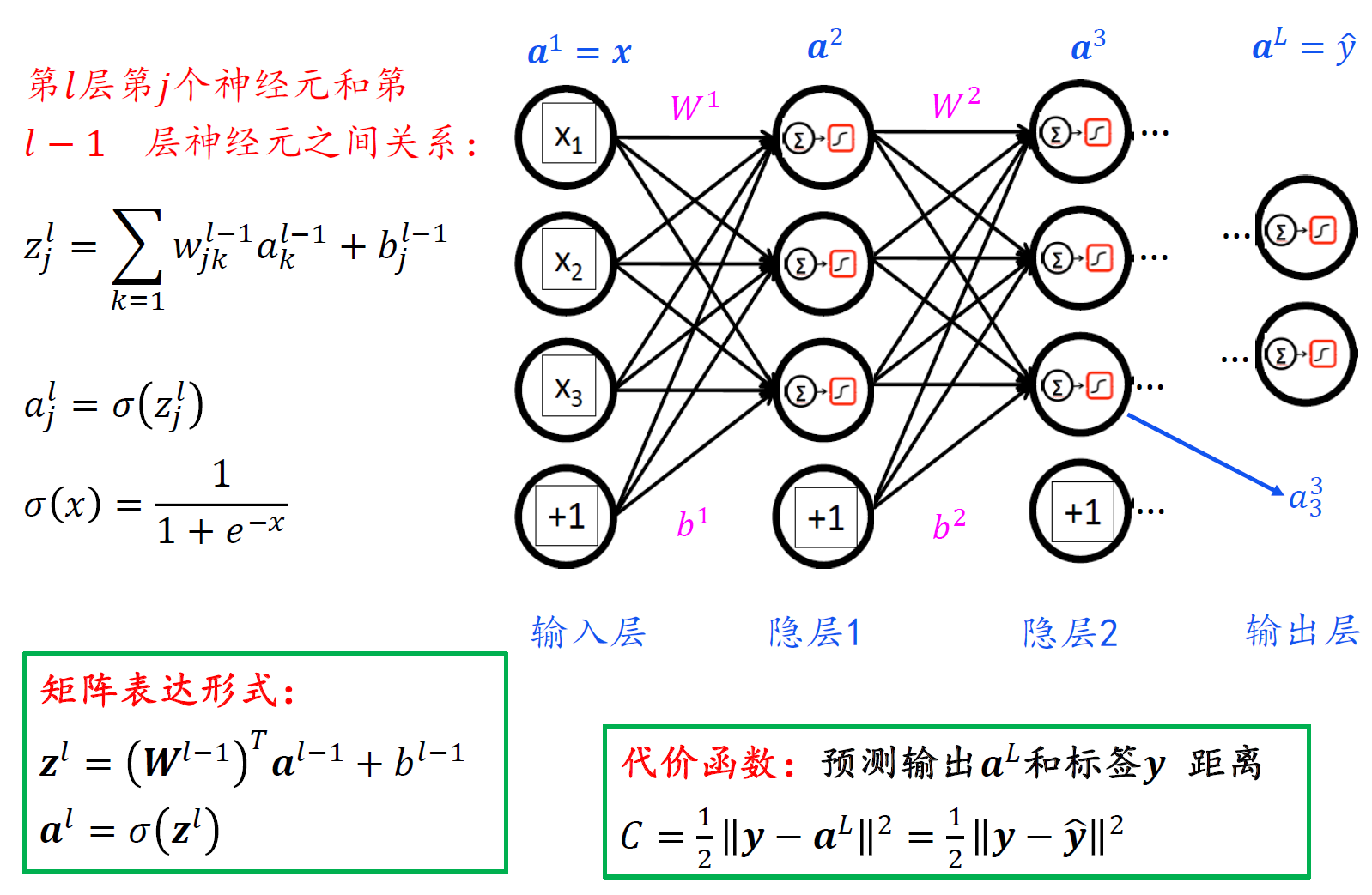

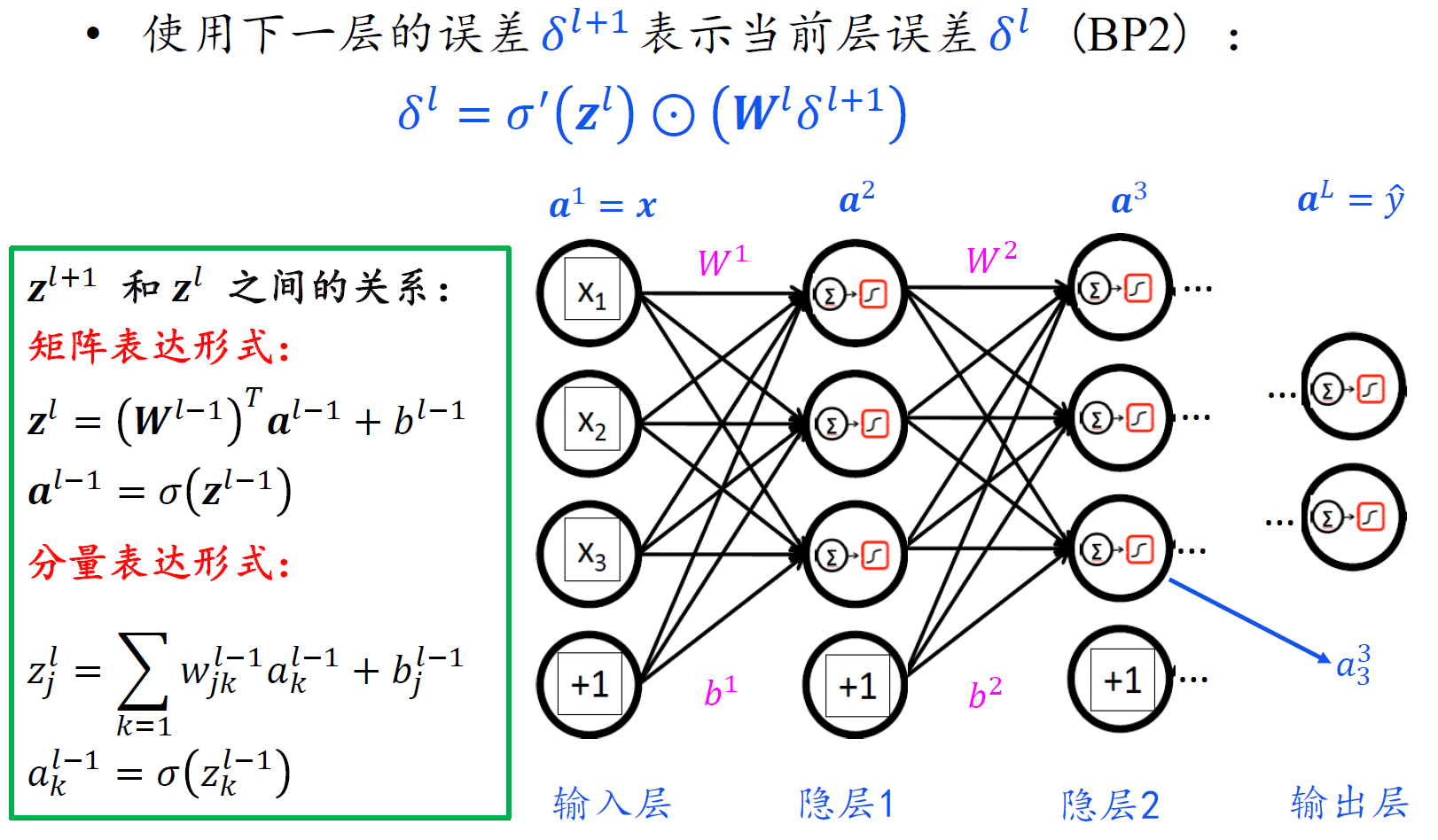

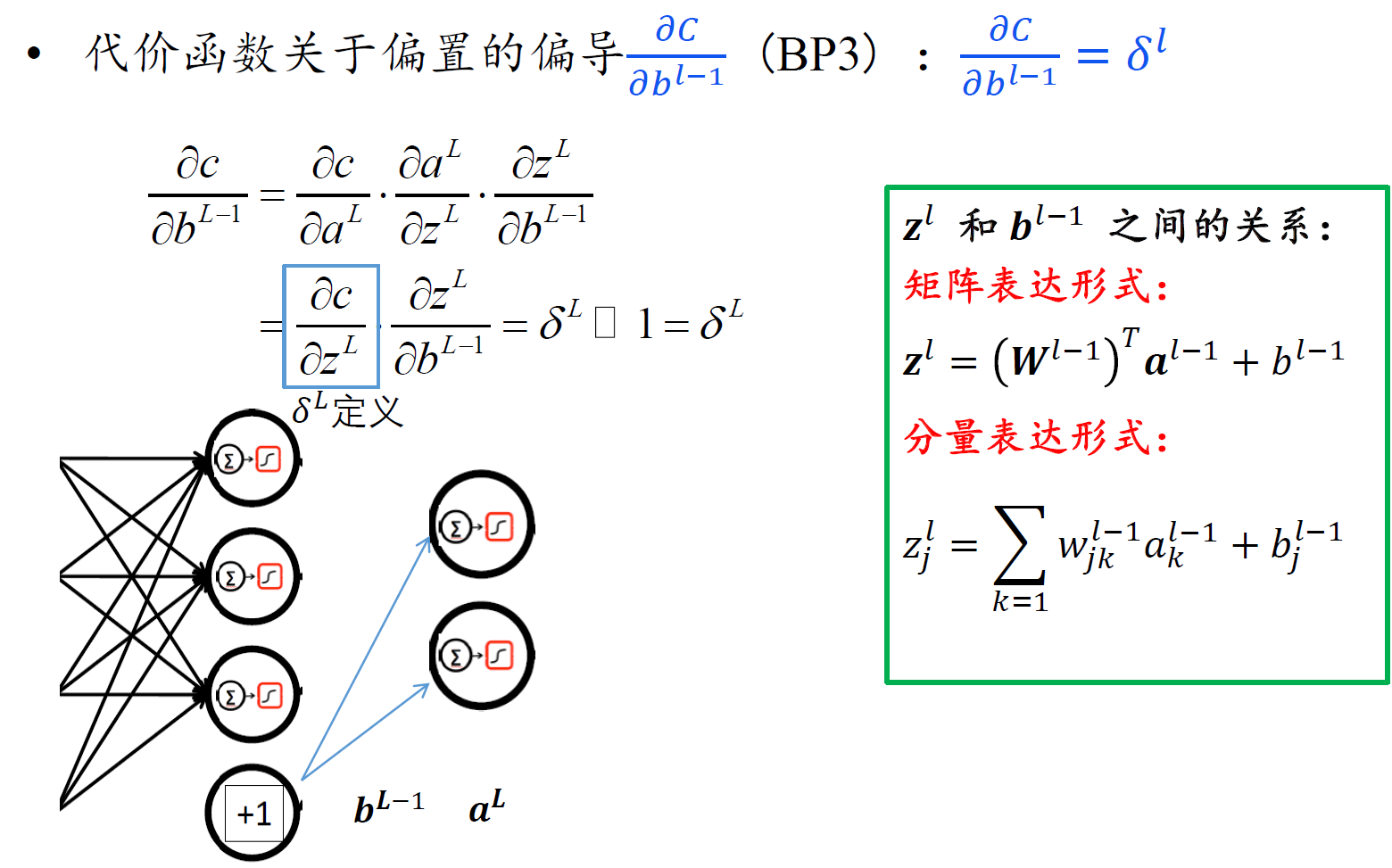
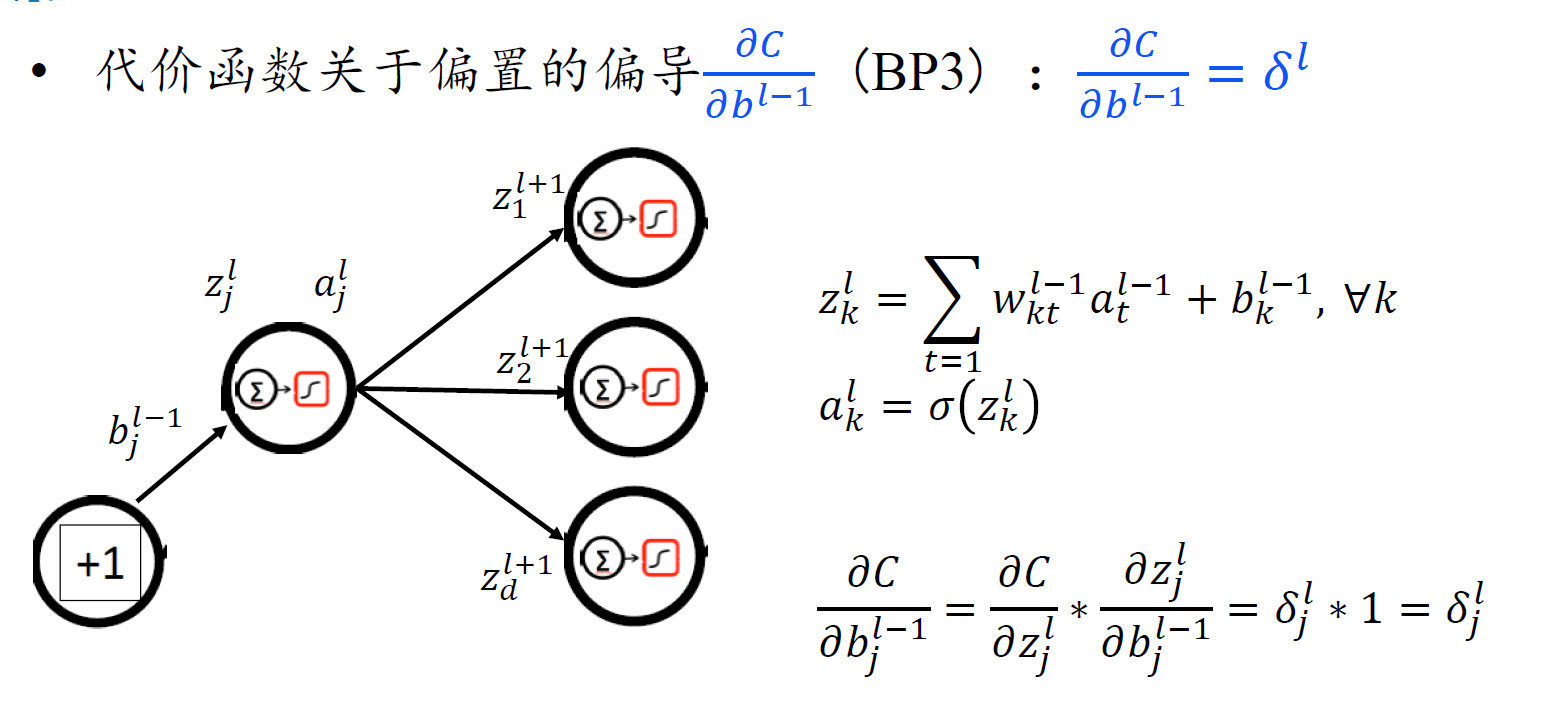
- 注意,由于$z^l$是关于l-1层权重和偏置的函数,所以对$b^{l-1}$ 求偏导,链式法则前面应该是对l层的z求偏导。
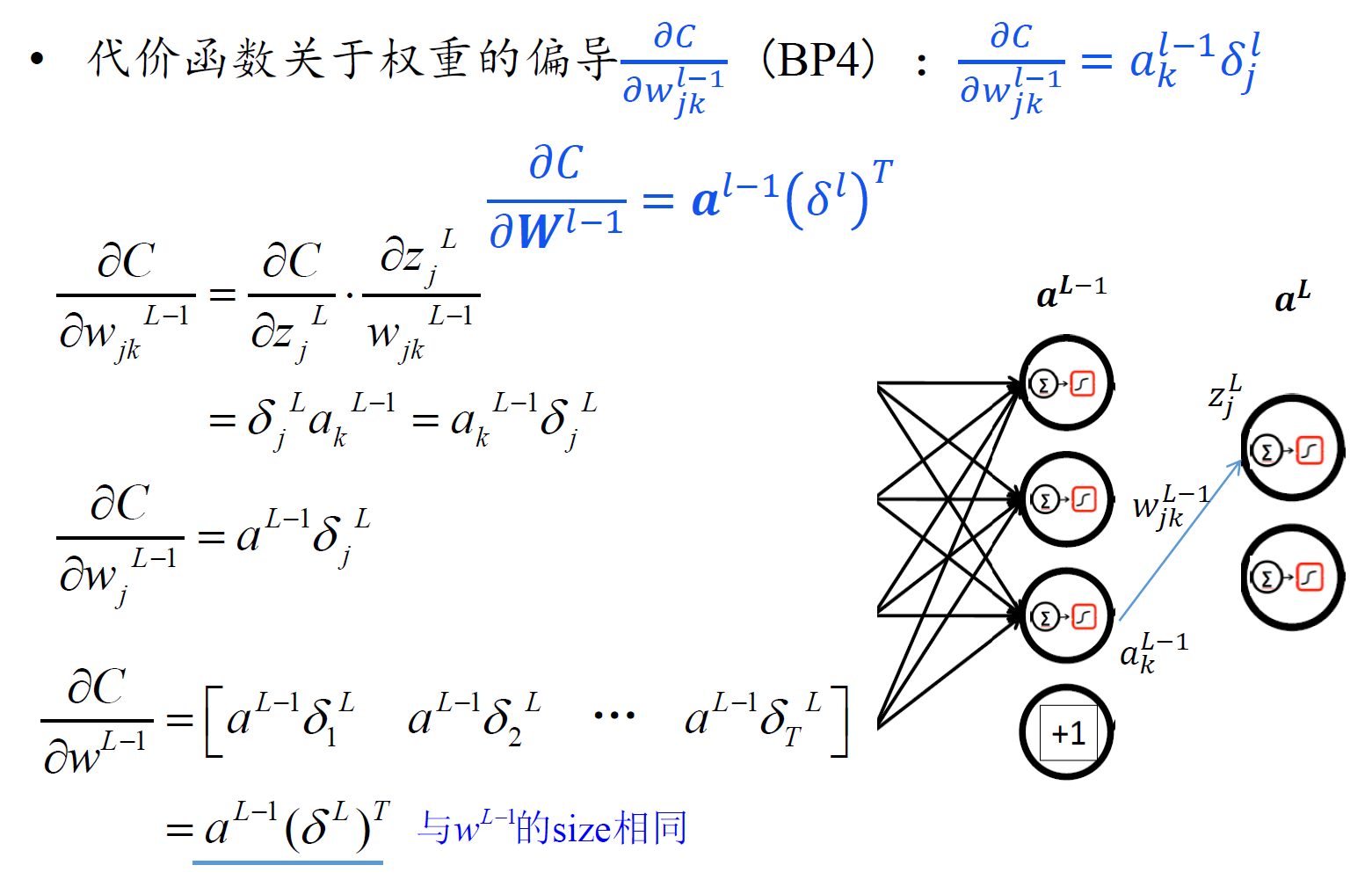
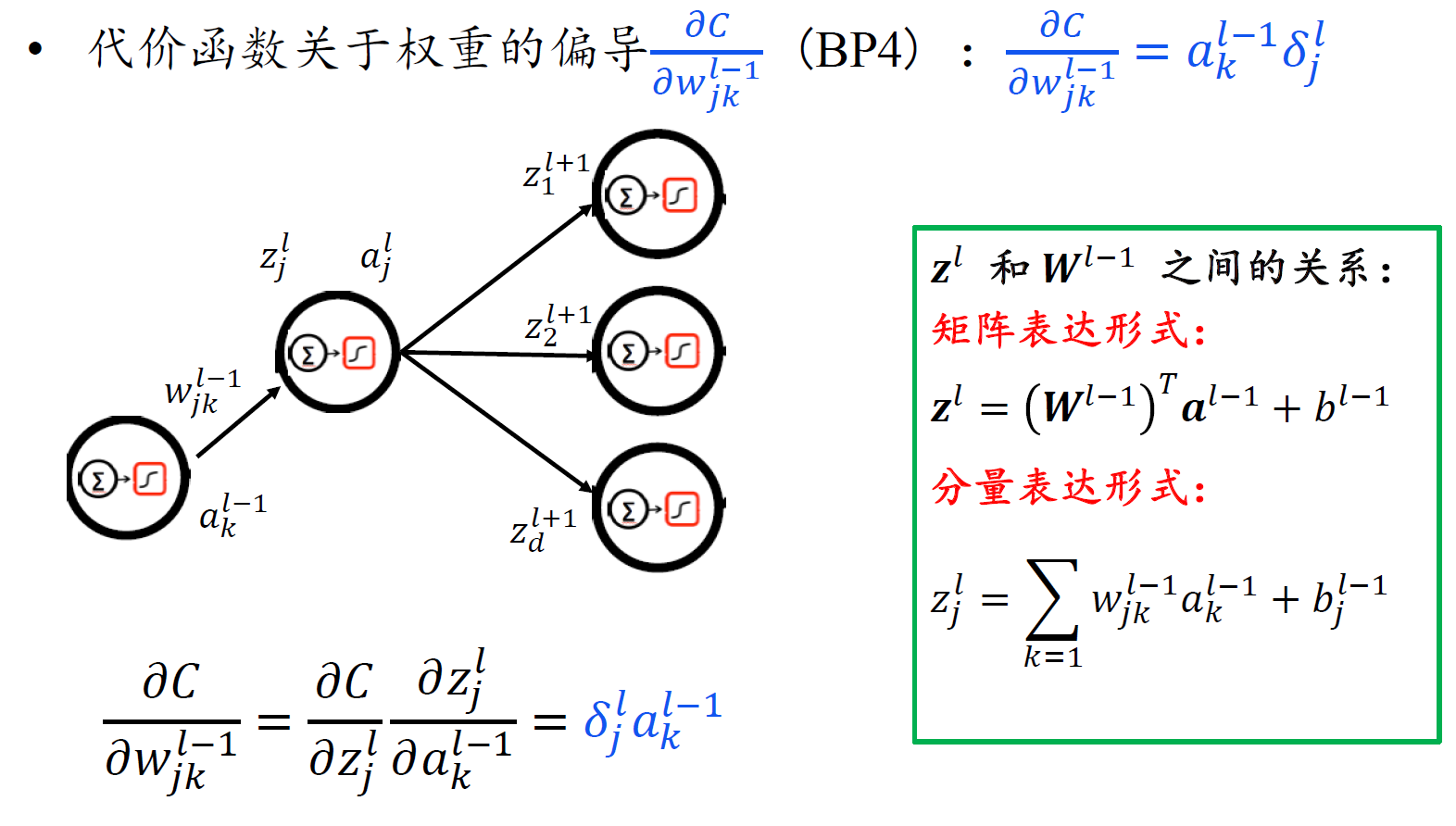
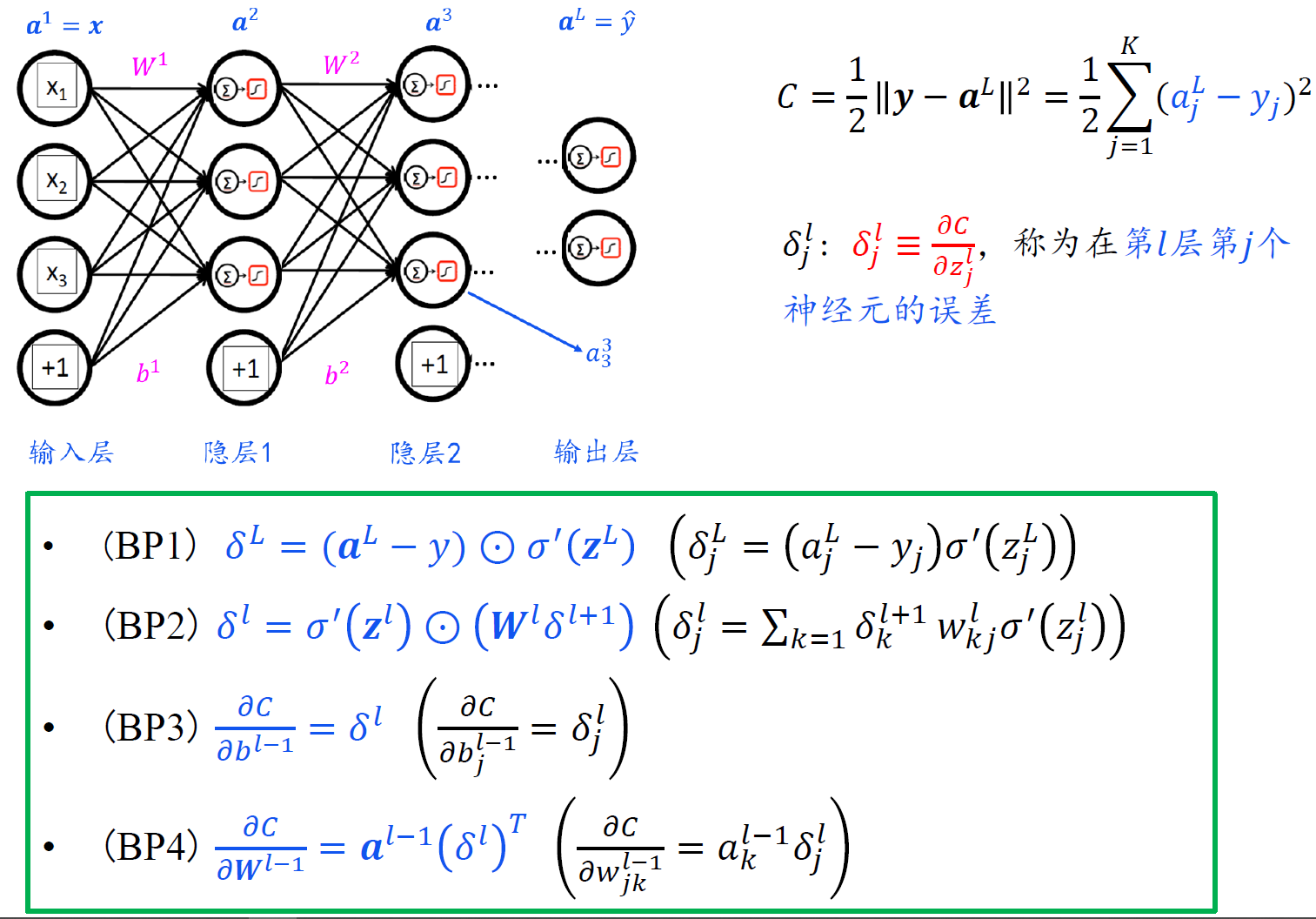
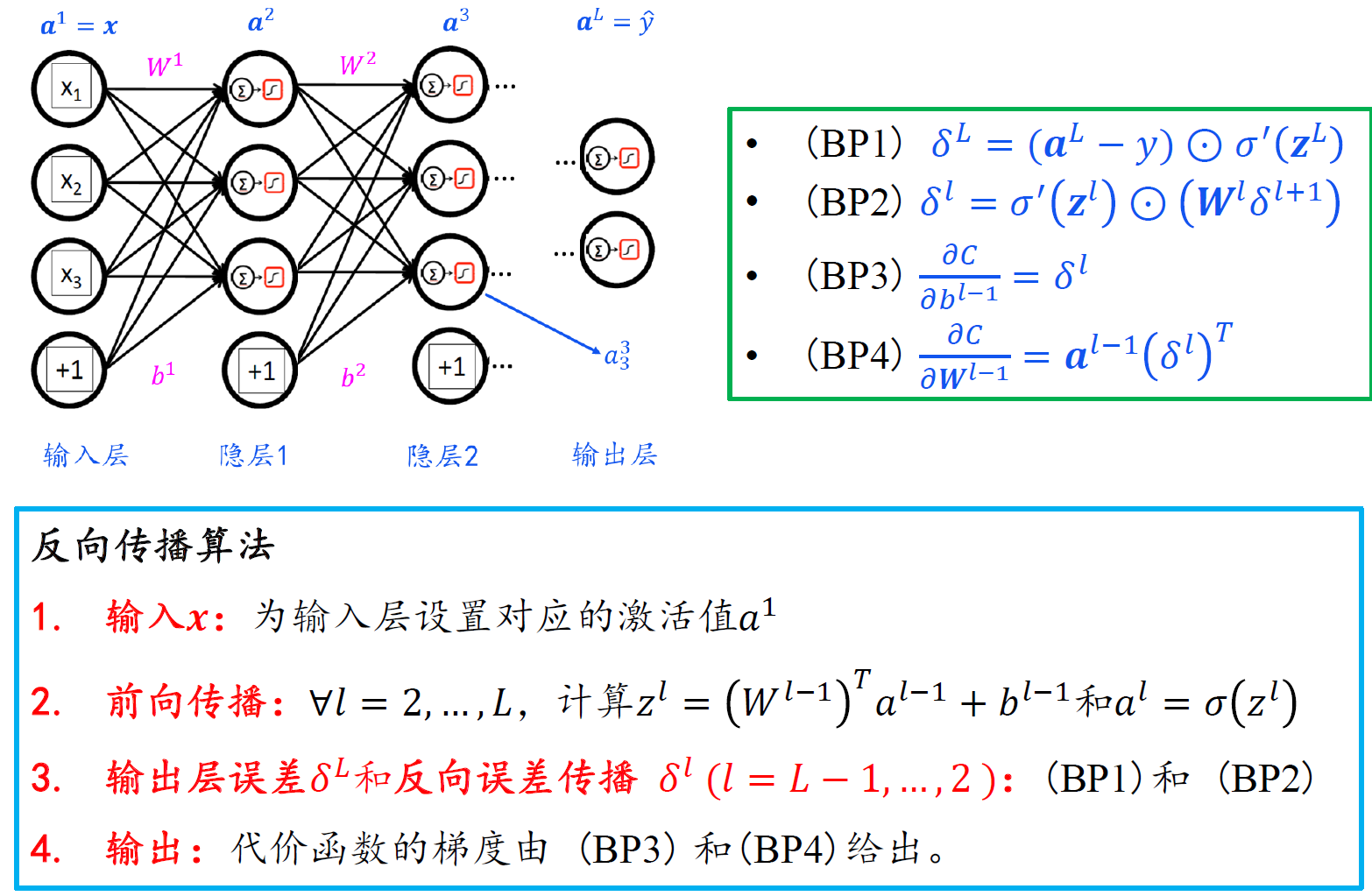
神经网络模型算法

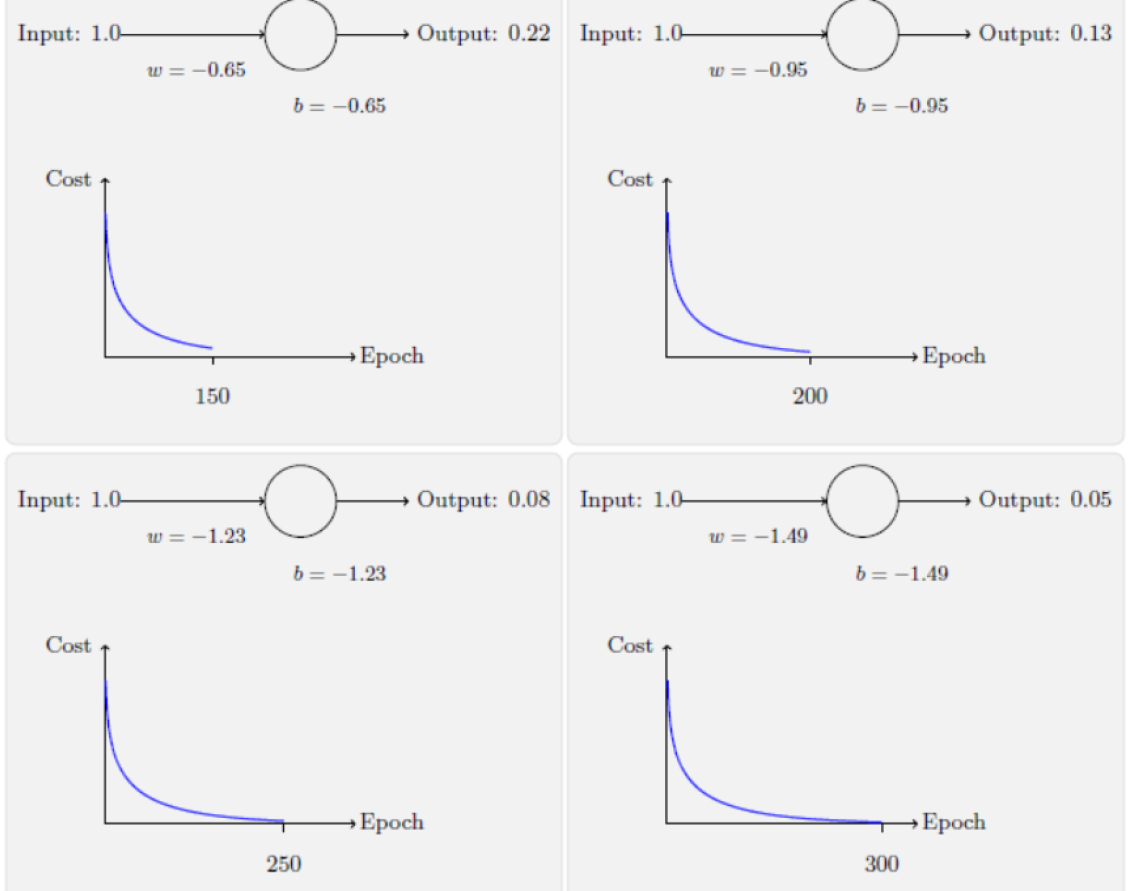
对数似然vs二次代价
二次代价:刚开始学习的速度比较缓慢
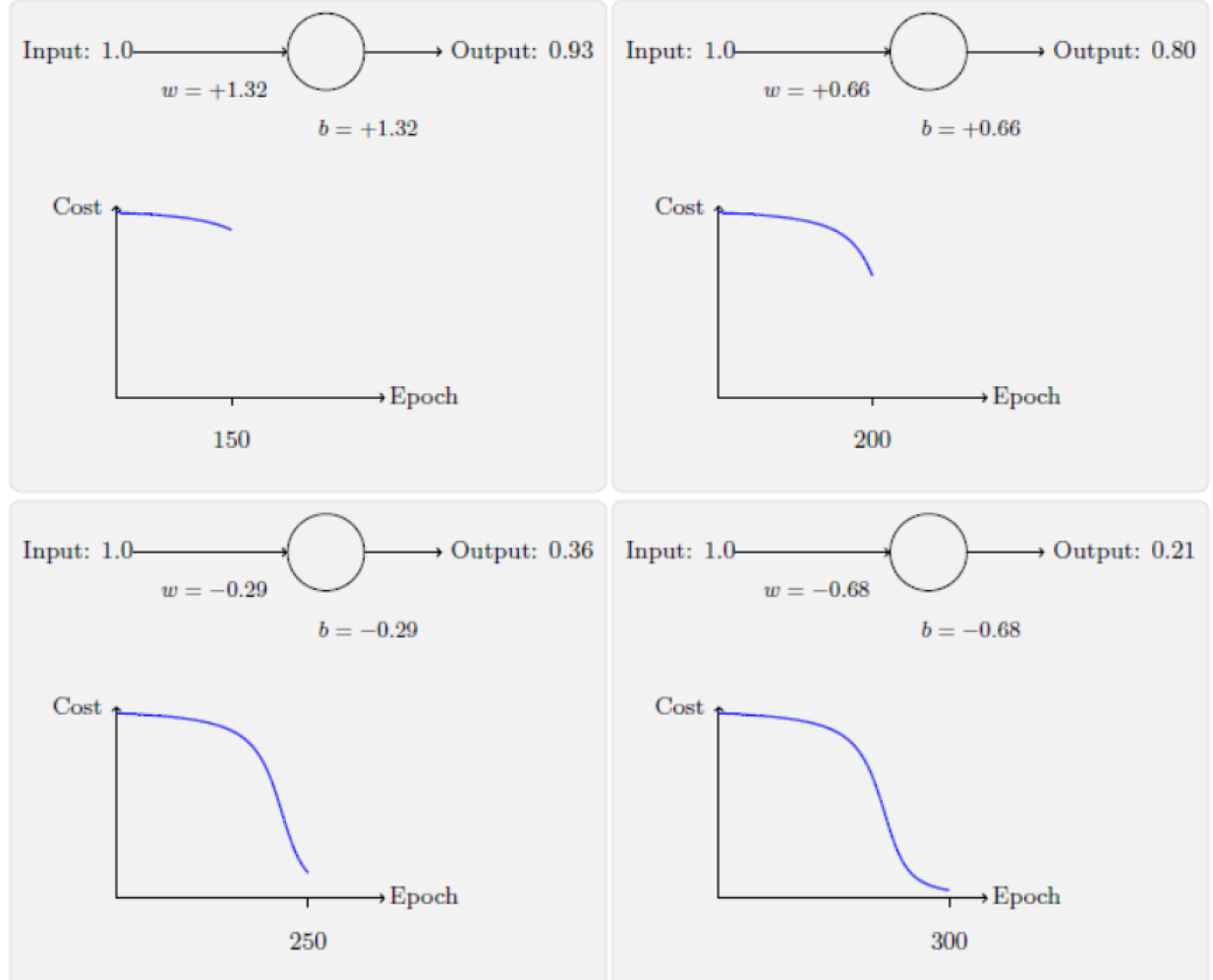
交叉熵:刚开始学习的速度相当快,与期待一样,当严重错误时能以最快速度学习;当预测输出接近正确输出时,学习速度变慢
三、支持向量机
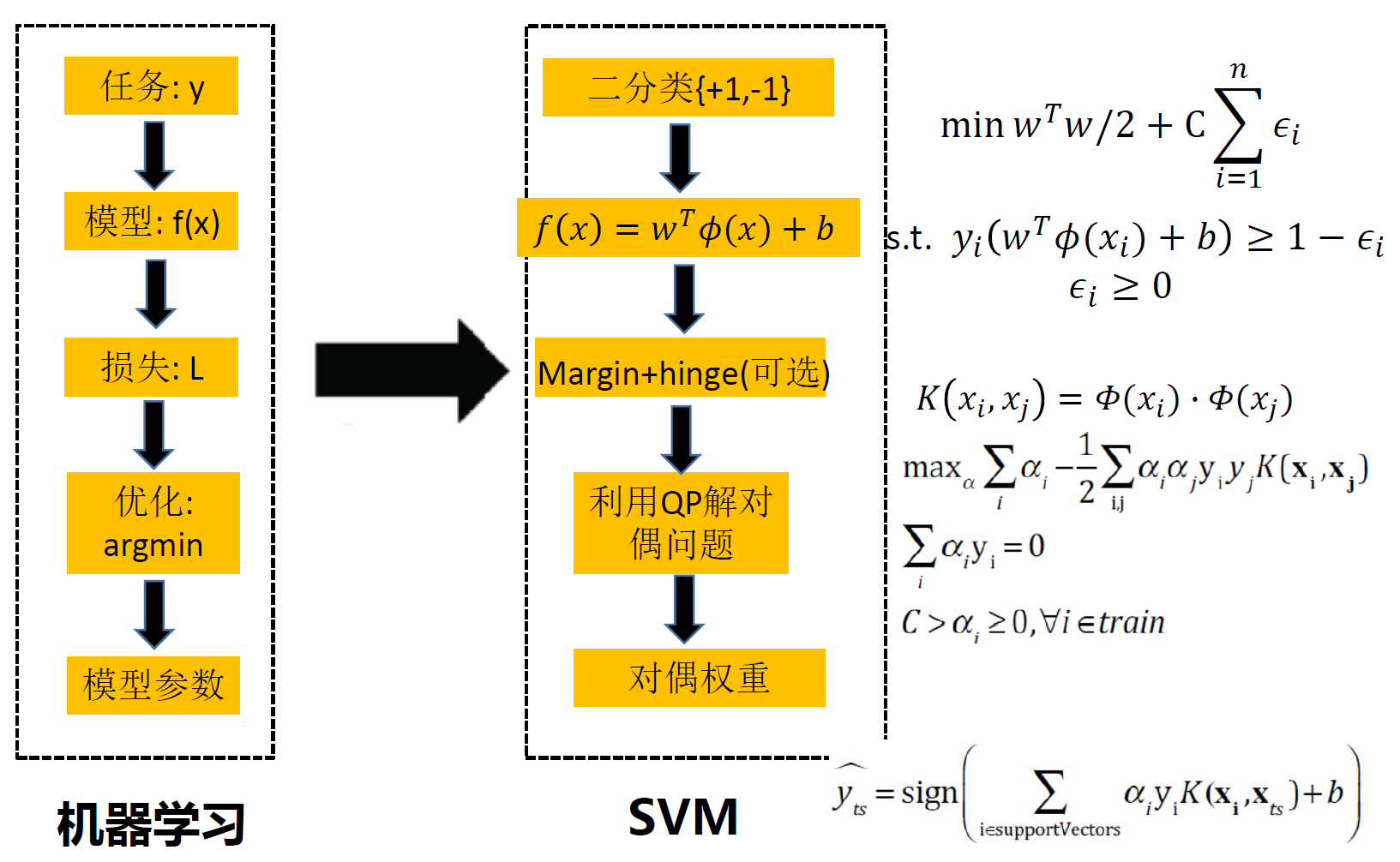
问题建模

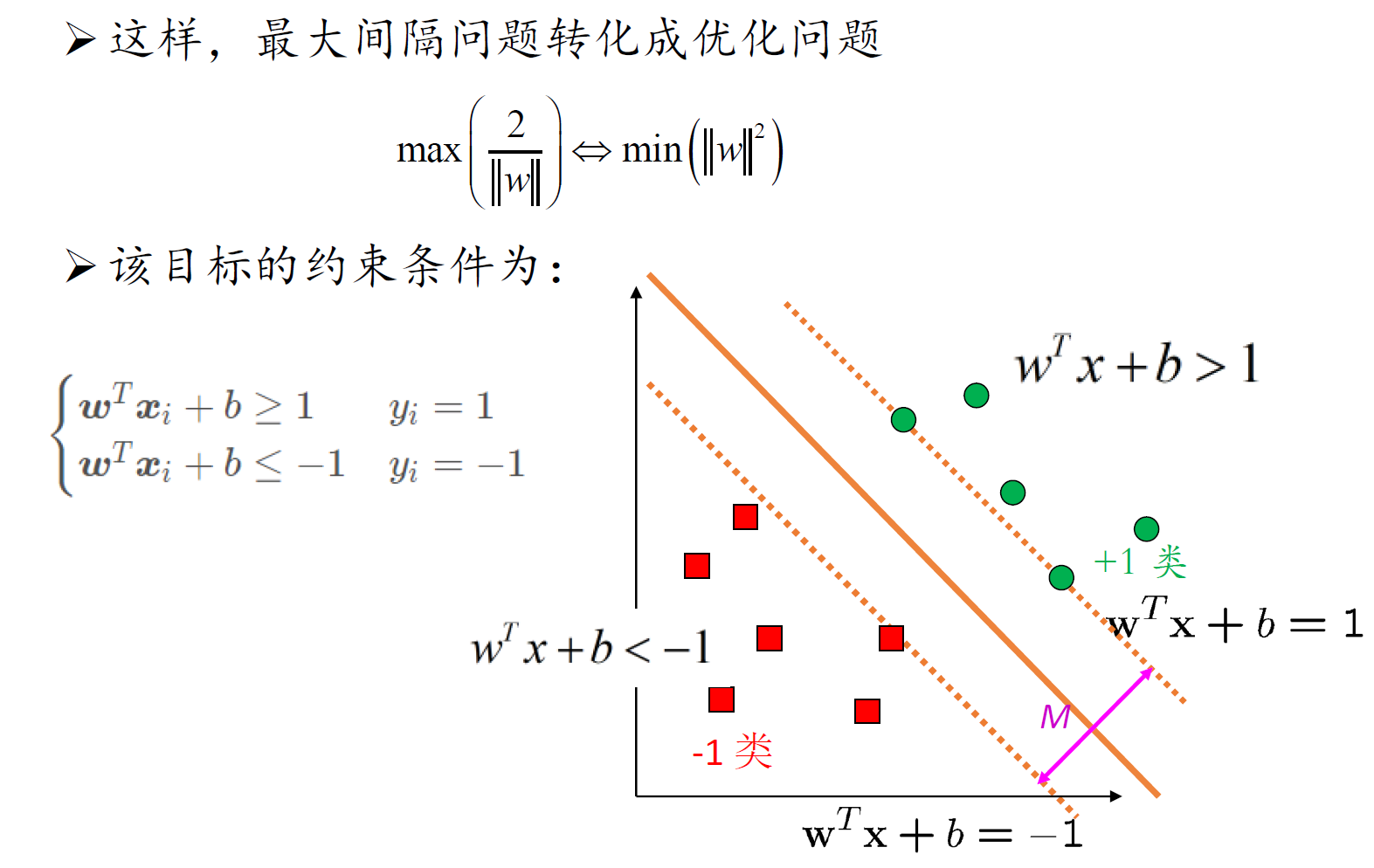

求解
约束优化、对偶




SVM对偶问题
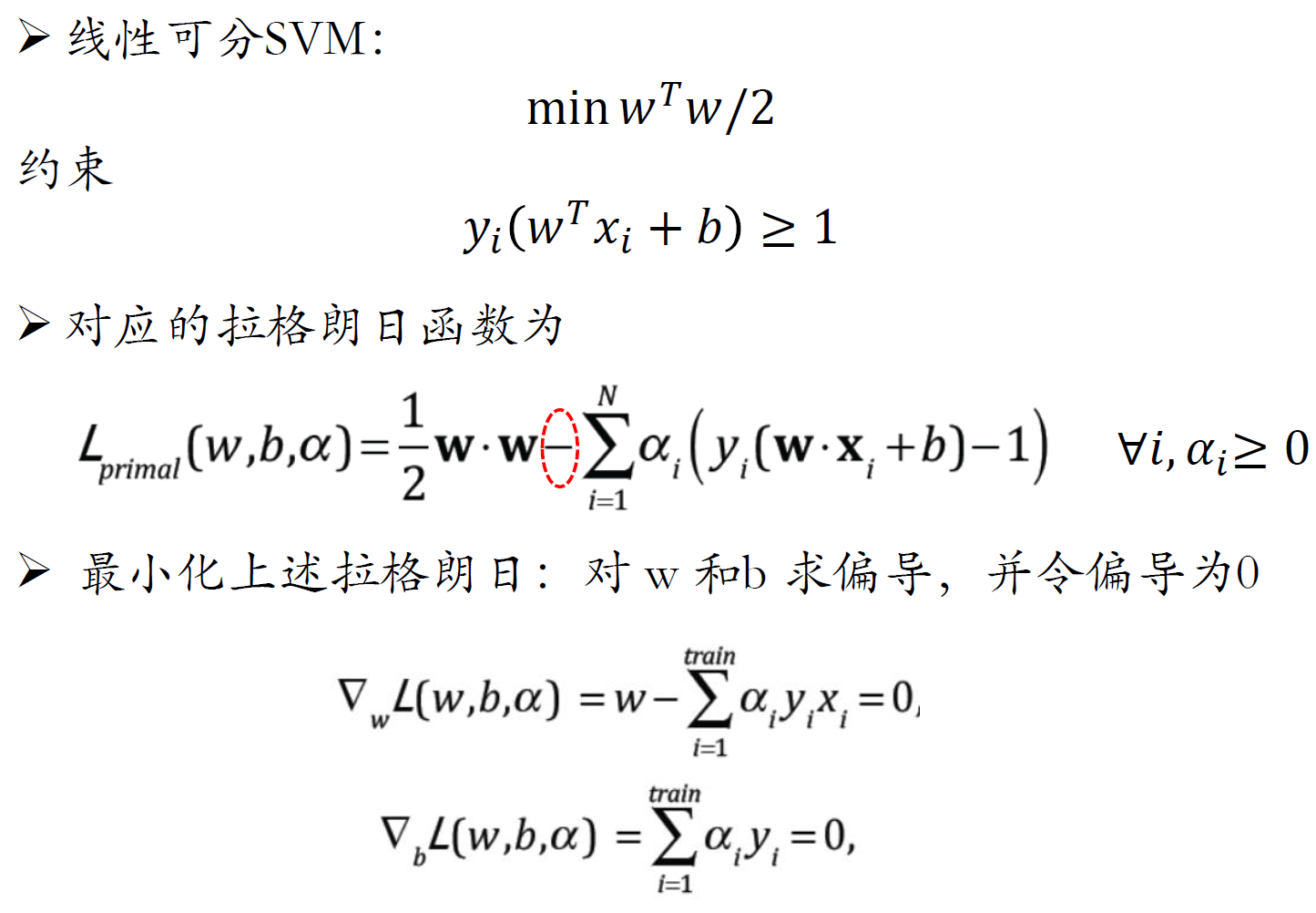
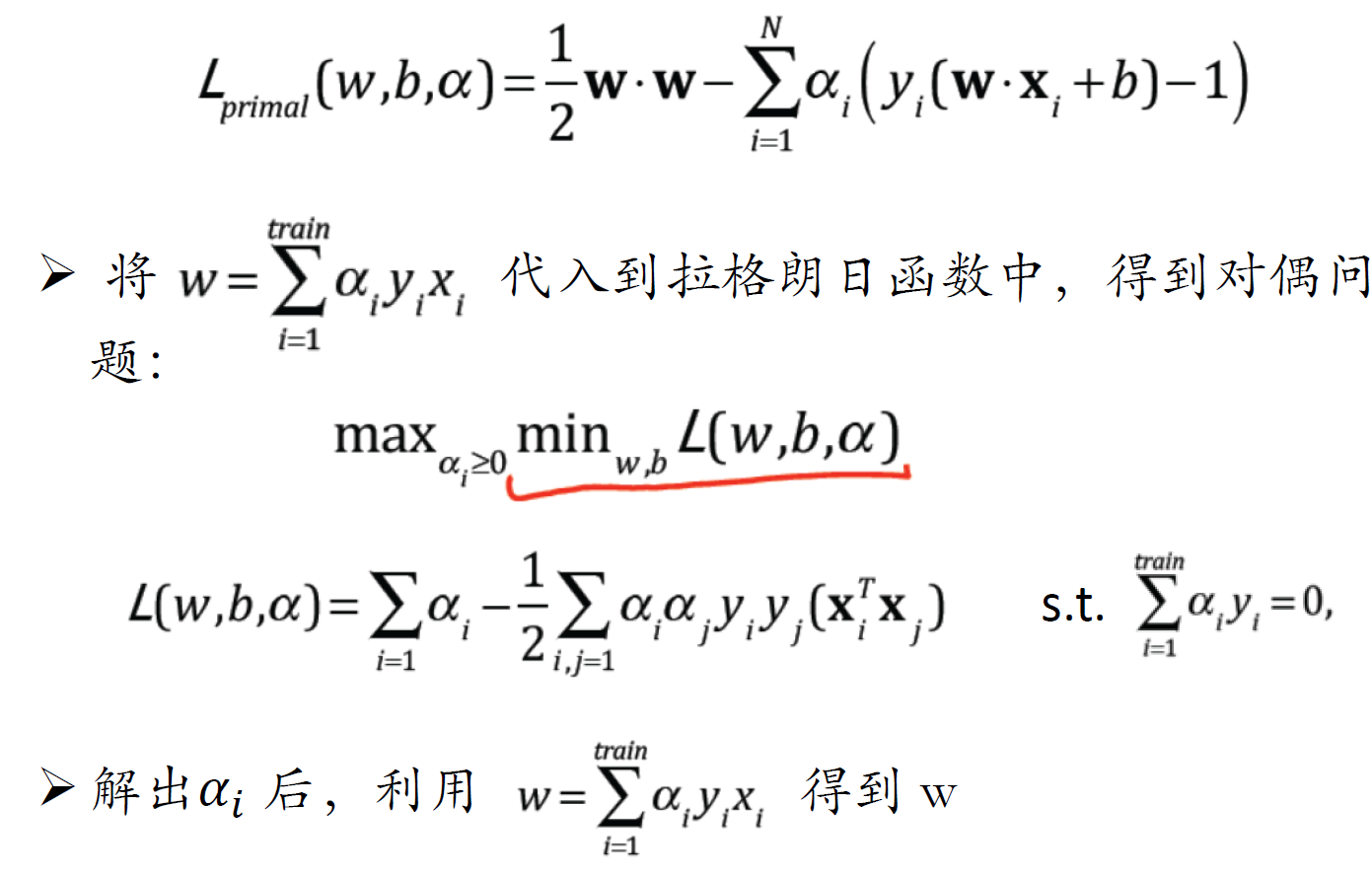
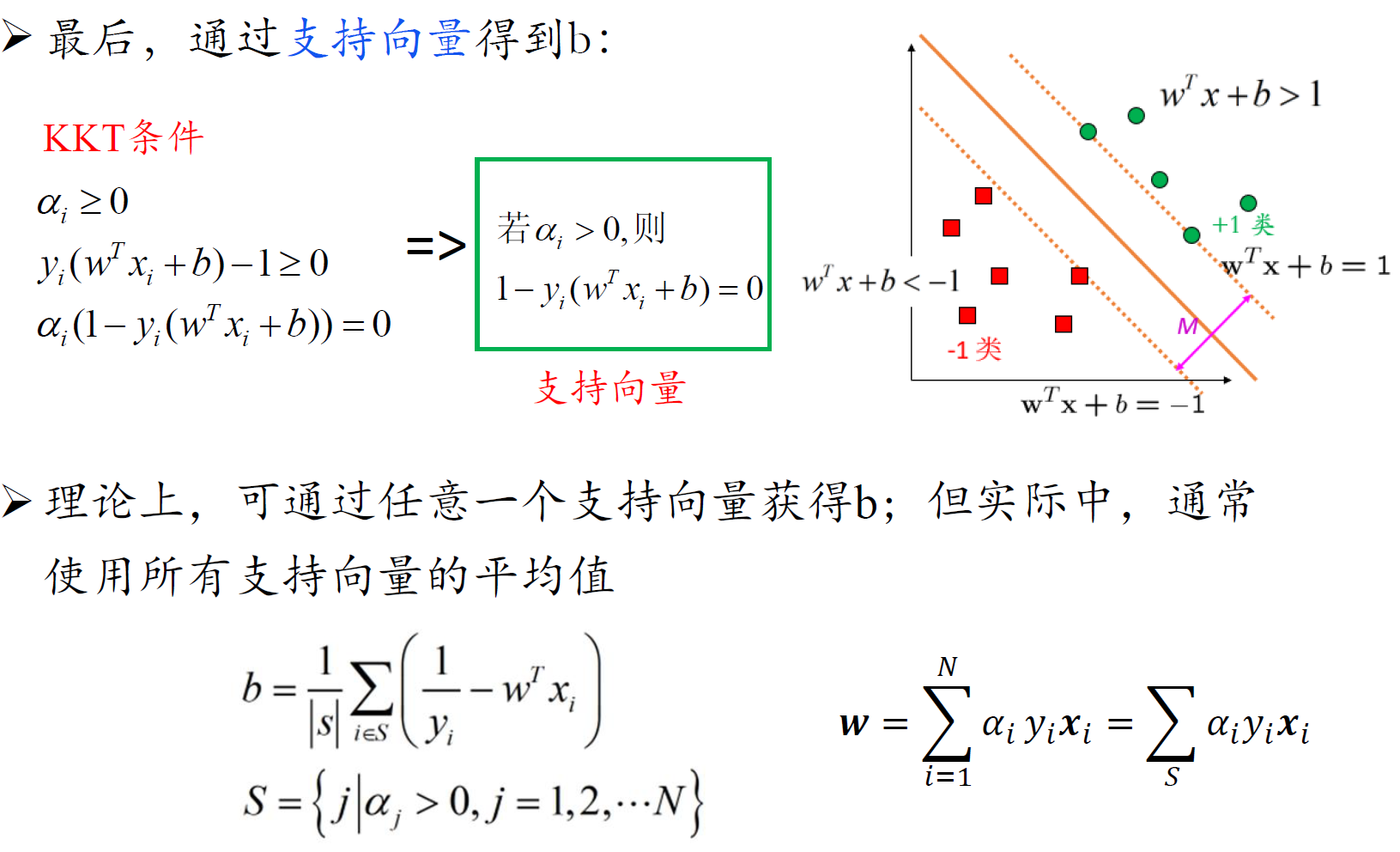
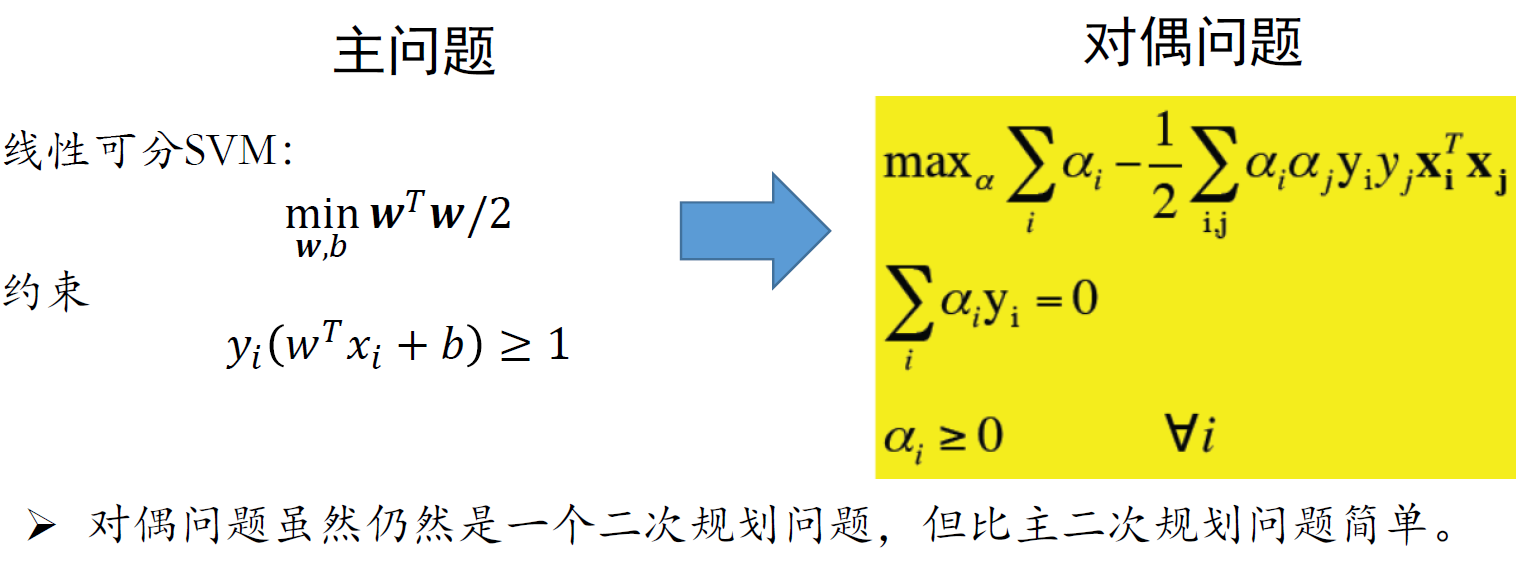
- 对偶问题的规模正比于训练样本数

例子
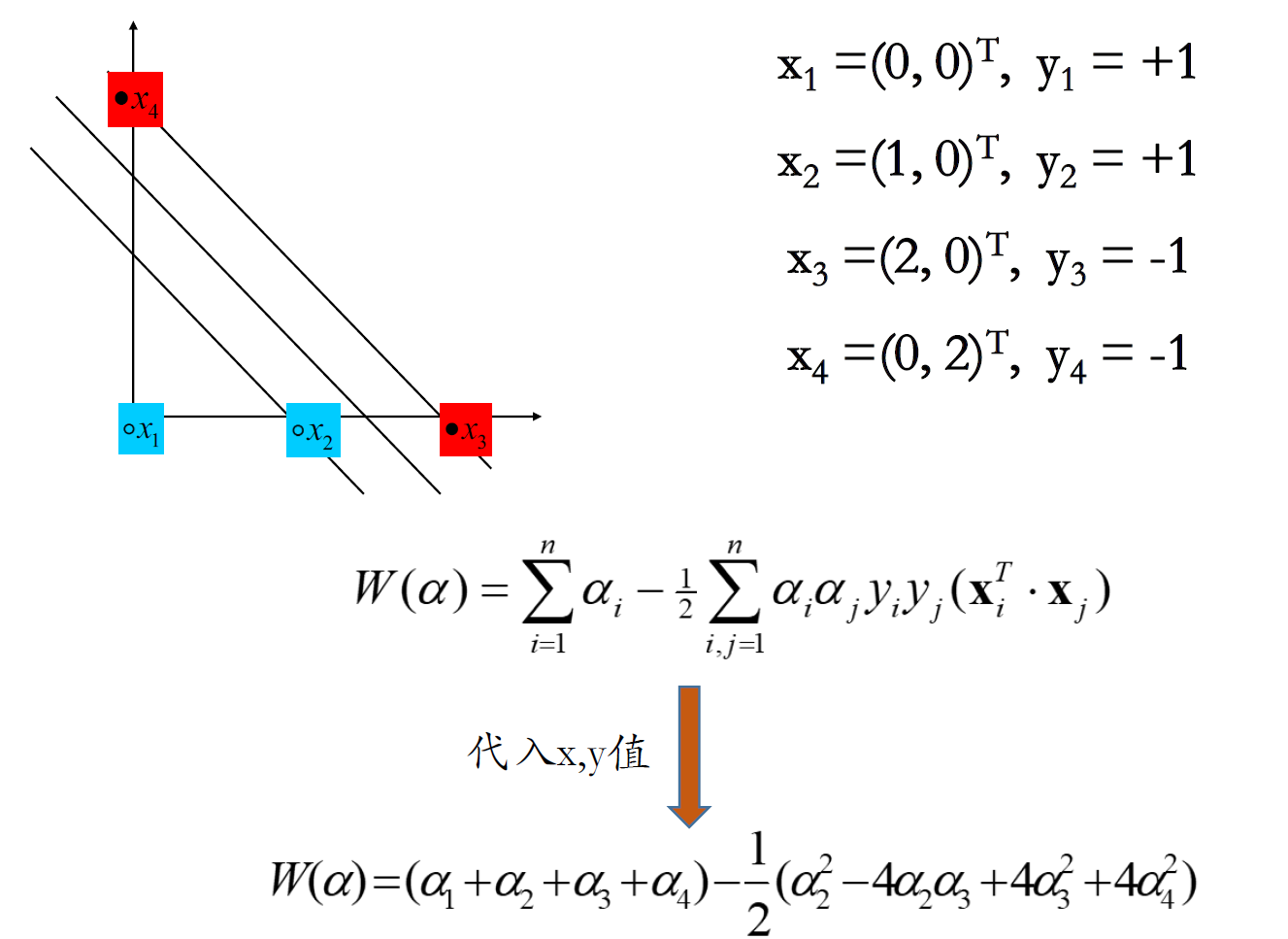

- 超平面法向量是支持向量的线性组合:仅支持向量的 $\alpha_i \neq0$
SVM性质

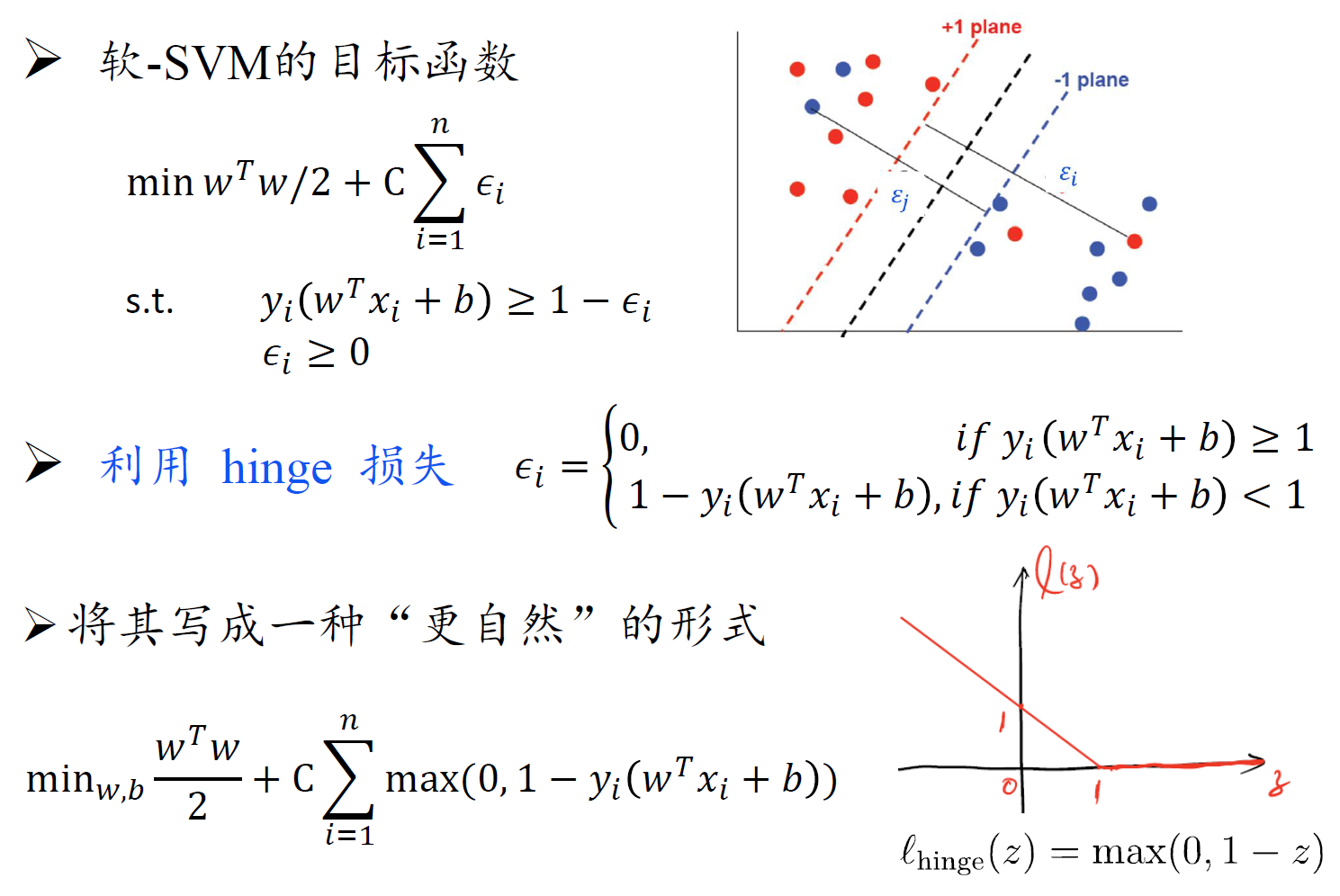
软SVM
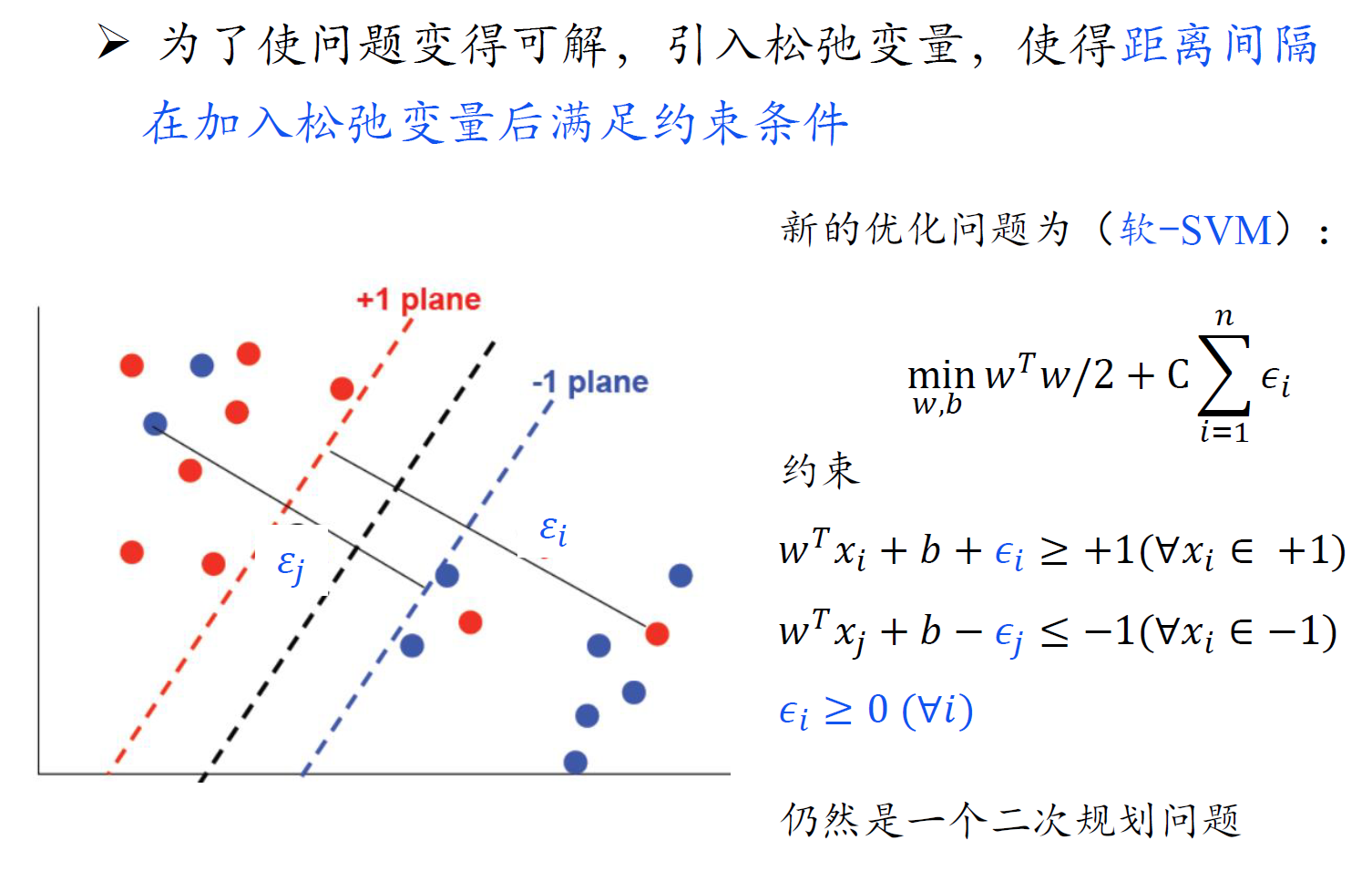
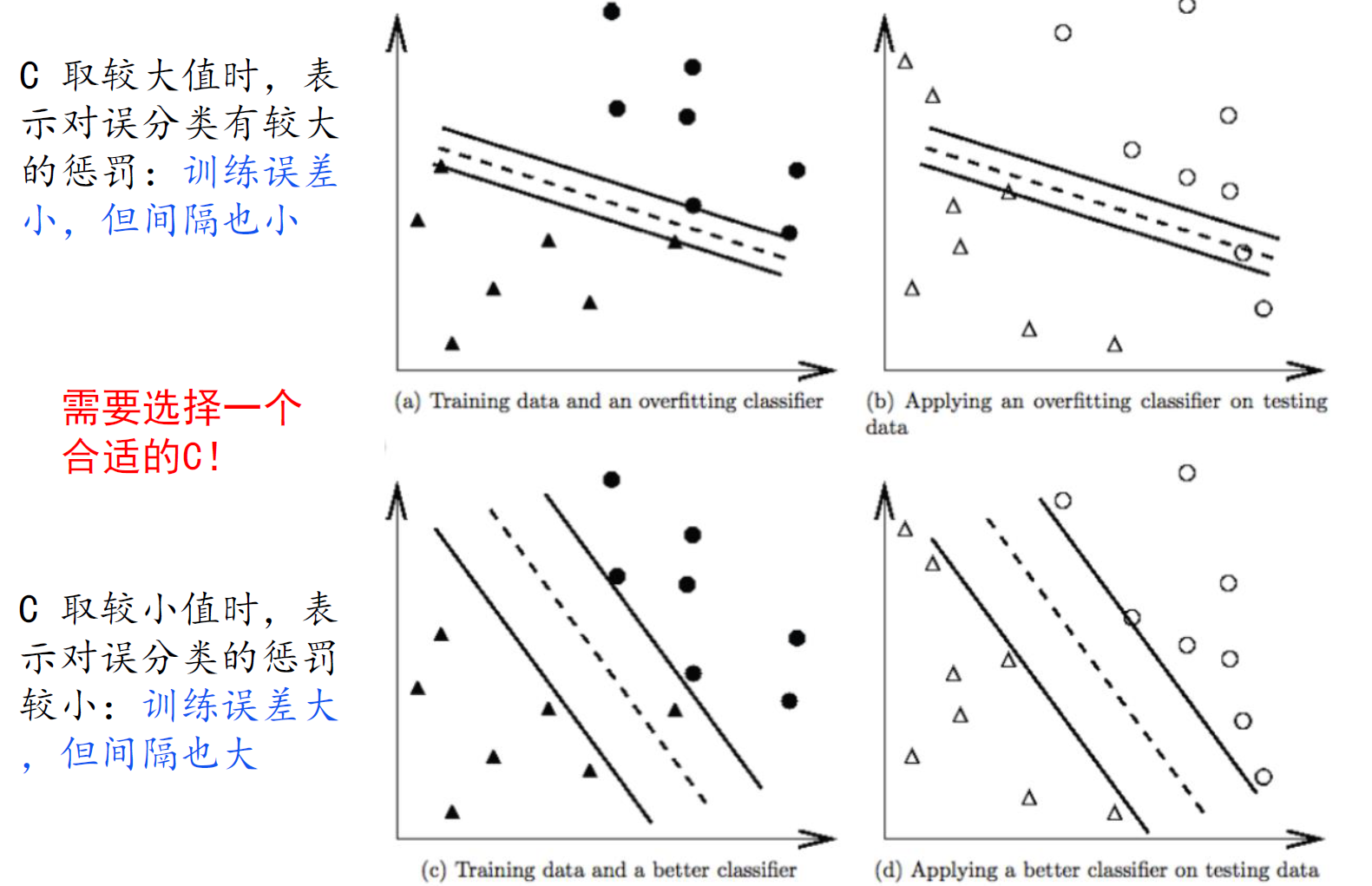

- 注意,软SVM主问题中的约束多了一个 $\epsilon_i \geq 0$
软SVM对偶问题推导
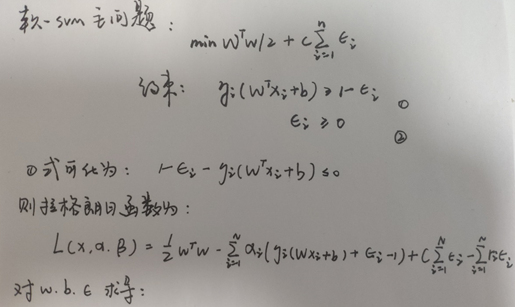


软SVM高效求解





四、集成学习、特征选择
集成学习
集成方法分类
- 串行式集成学习 :个体学习器之间存在强依赖关系,后生成的个体学习器依赖前面生成的个体学习器。代表
性算法 Boosting。 - 并行式集成学习方法: 个体学习器之间不存在强依赖关系,代表是 Bagging和随机森林
重采样方法
- 随机采样:在原来的数据集上随机采样一个子集,得到新的训练集,这就是 Bagging 族方法的做法。
- 带权采样:采样时,可以给训练集里的每个元素不同的权,权值通过上一次训练的结果来确定。这就是
Boosting 族方法的做法。
AdaBoost
关注 被错分的样本 器重 性能好的弱分类器

Bagging


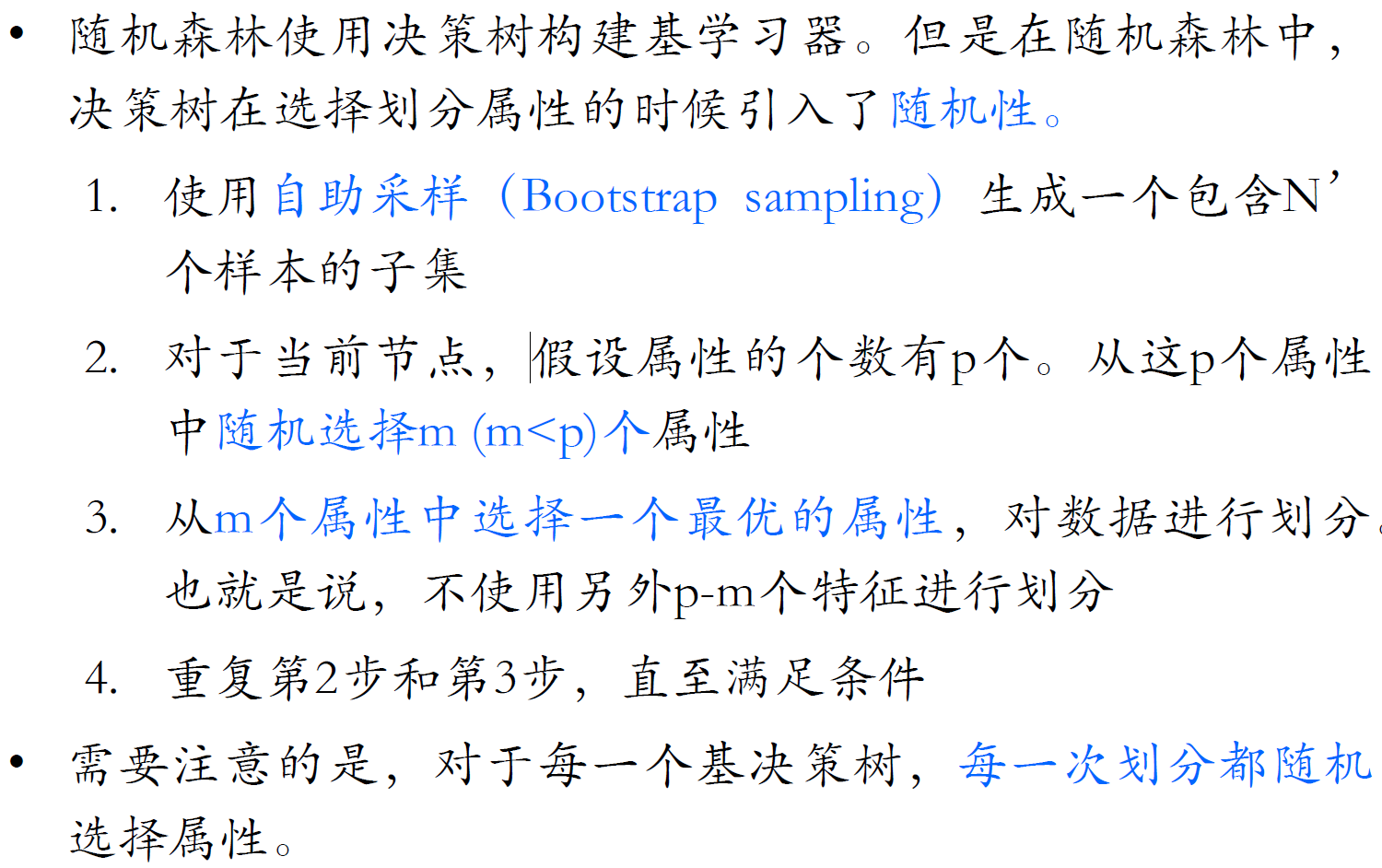
随机森林
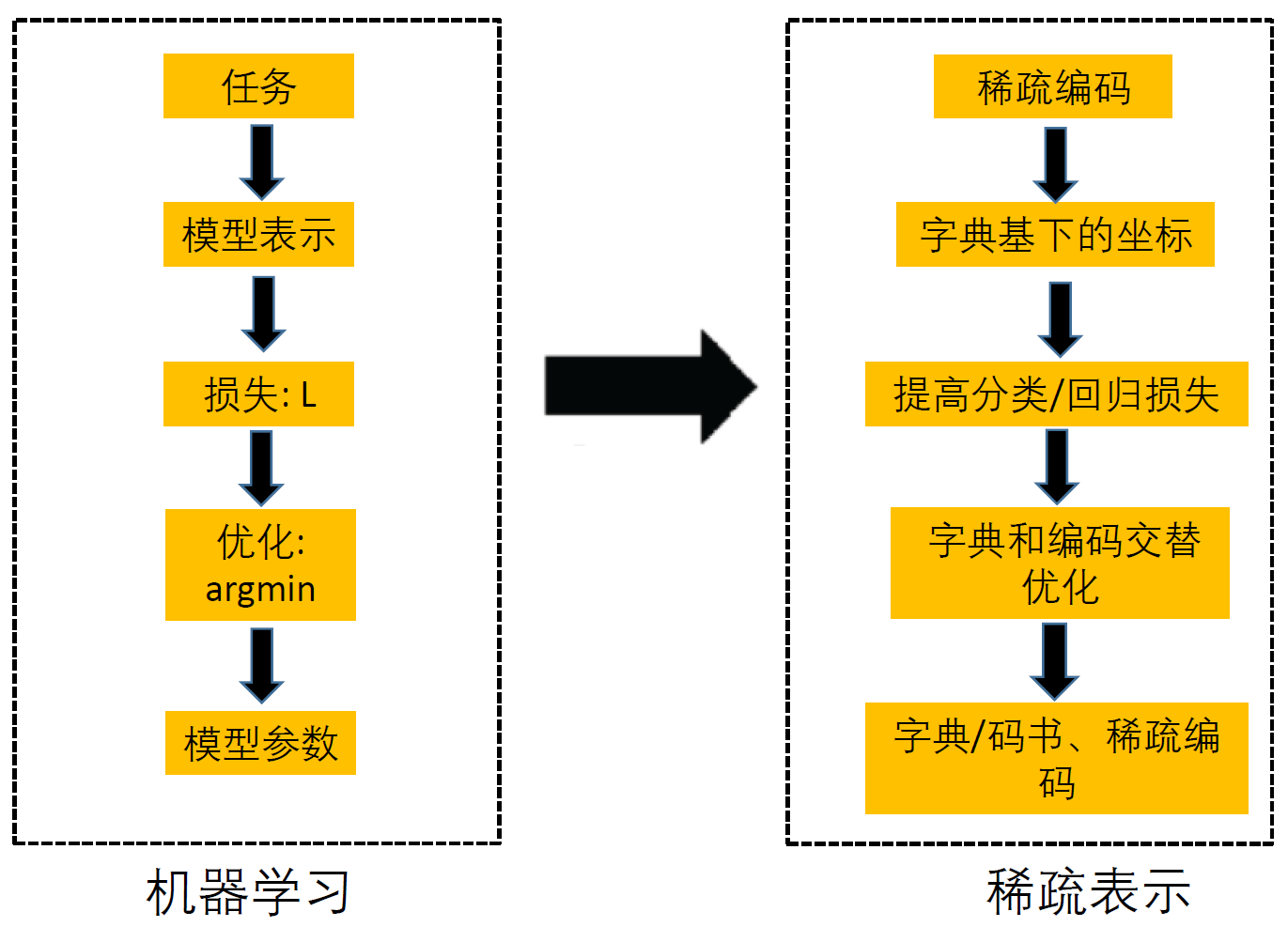
特征选择与稀疏学习
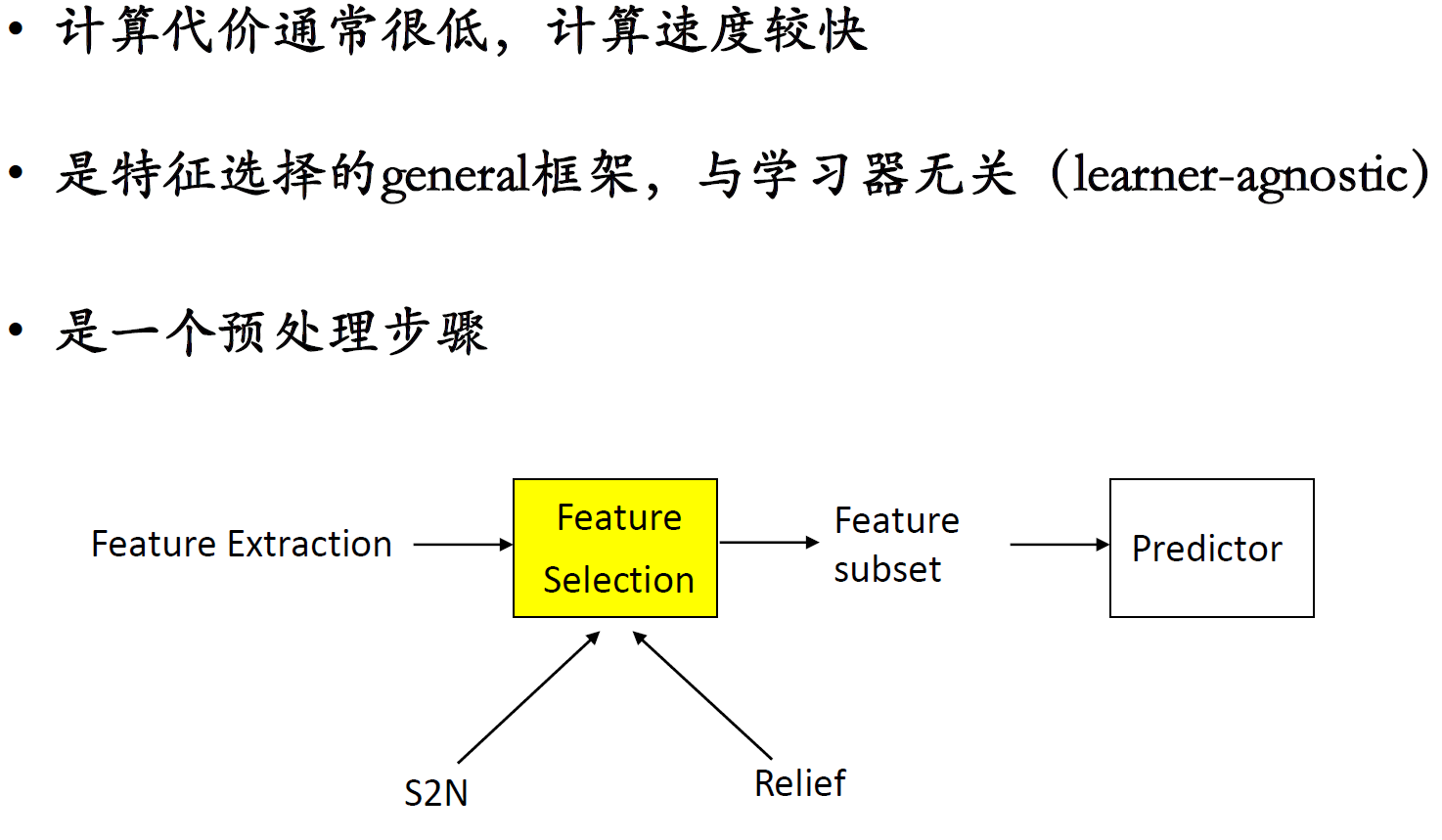
过滤式方法
- 单变量过滤方法:Singal-to-noise ratio (S2N)
- Relief
包裹式方法


嵌入式方法


Lasso回归

坐标下降法求解

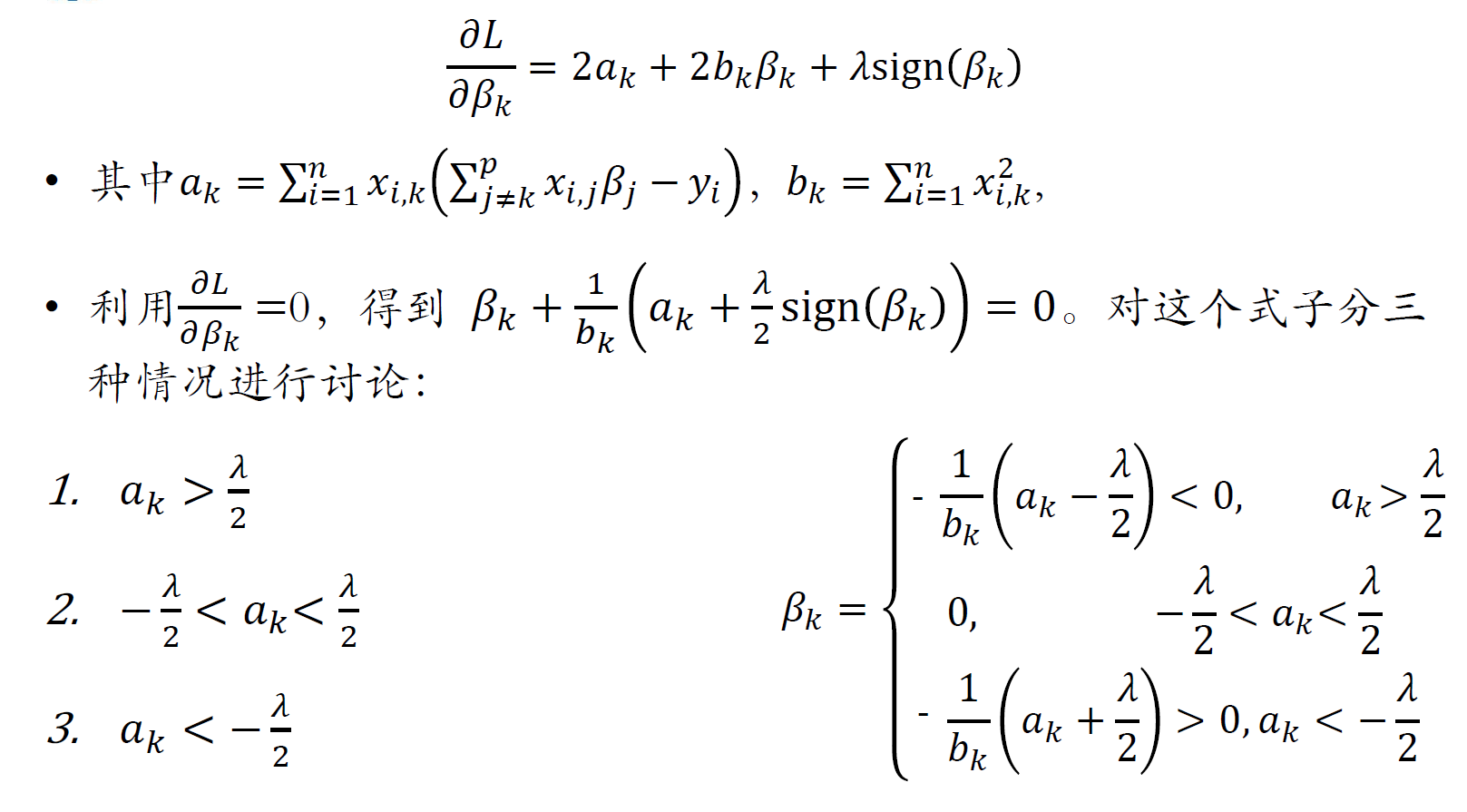
坐标下降法推导



综上有:

总结


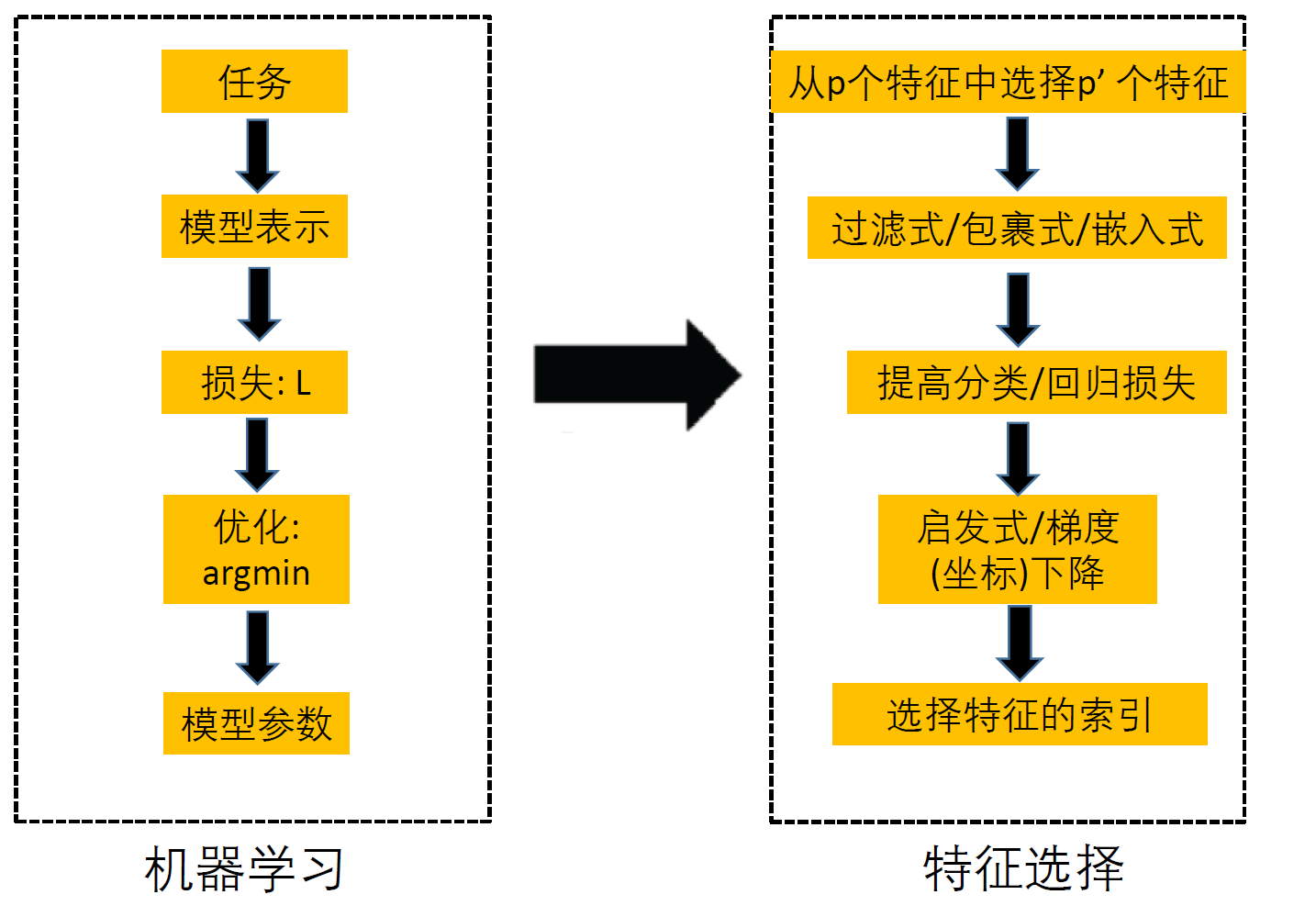
稀疏学习

xi为p*1维,B为p*k维,ai为k*1维,也就是将样本x从p维降到k维

五、非监督学习概述、贝叶斯分类器
聚类算法
- 层次聚类算法:自底而上:聚合;自顶而下:分裂
- 划分式聚类算法:给出随机化初始划分;对划分迭代优化:Kmeans、GMM
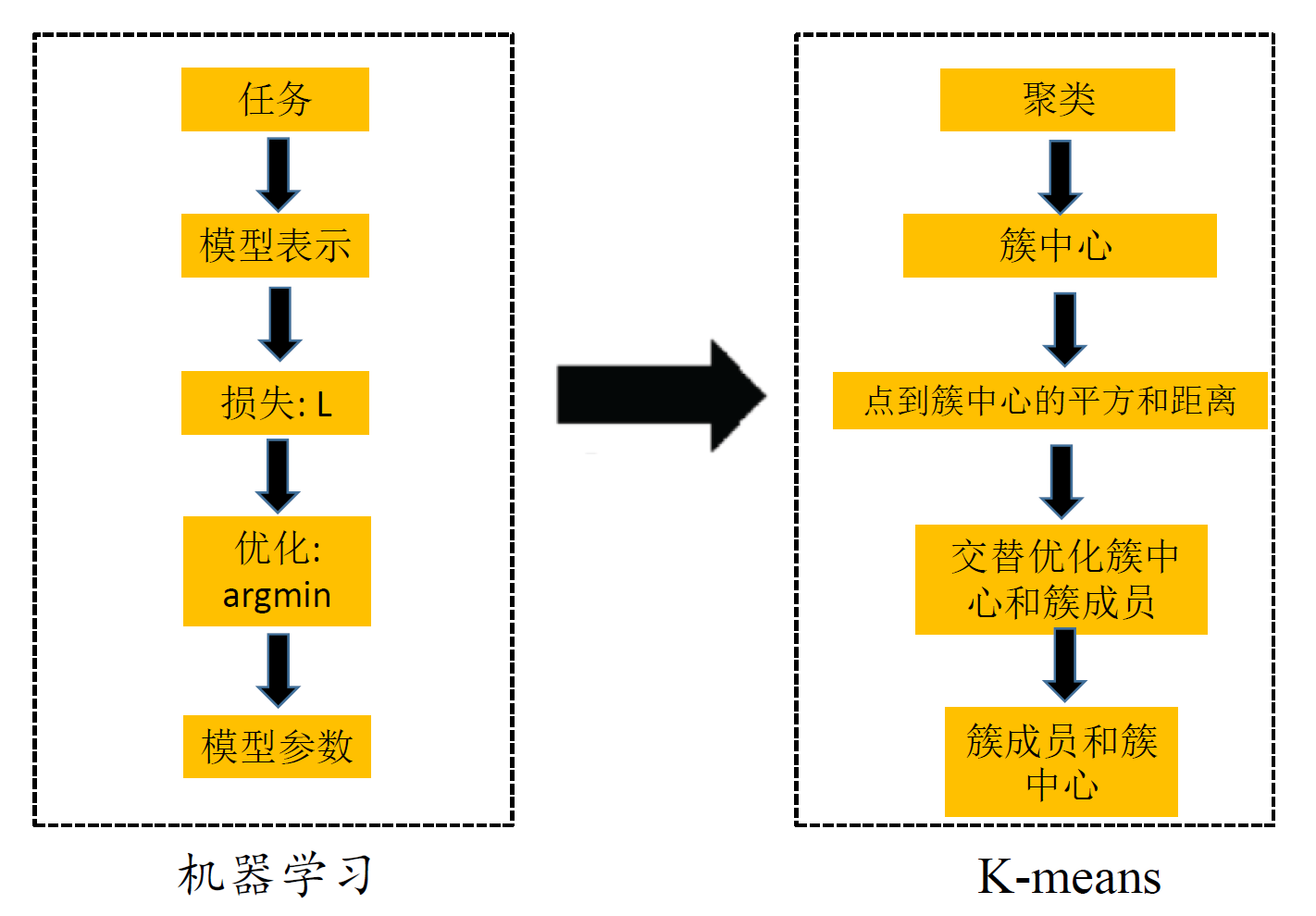
K-means






- 算法复杂度

- 聚类中心初值选择:
- 通过启发式方法选择好的初值:例如要求种子点之间有较大的距离
- 尝试多个初值 ,选择平方误差和最小的一组聚类结果
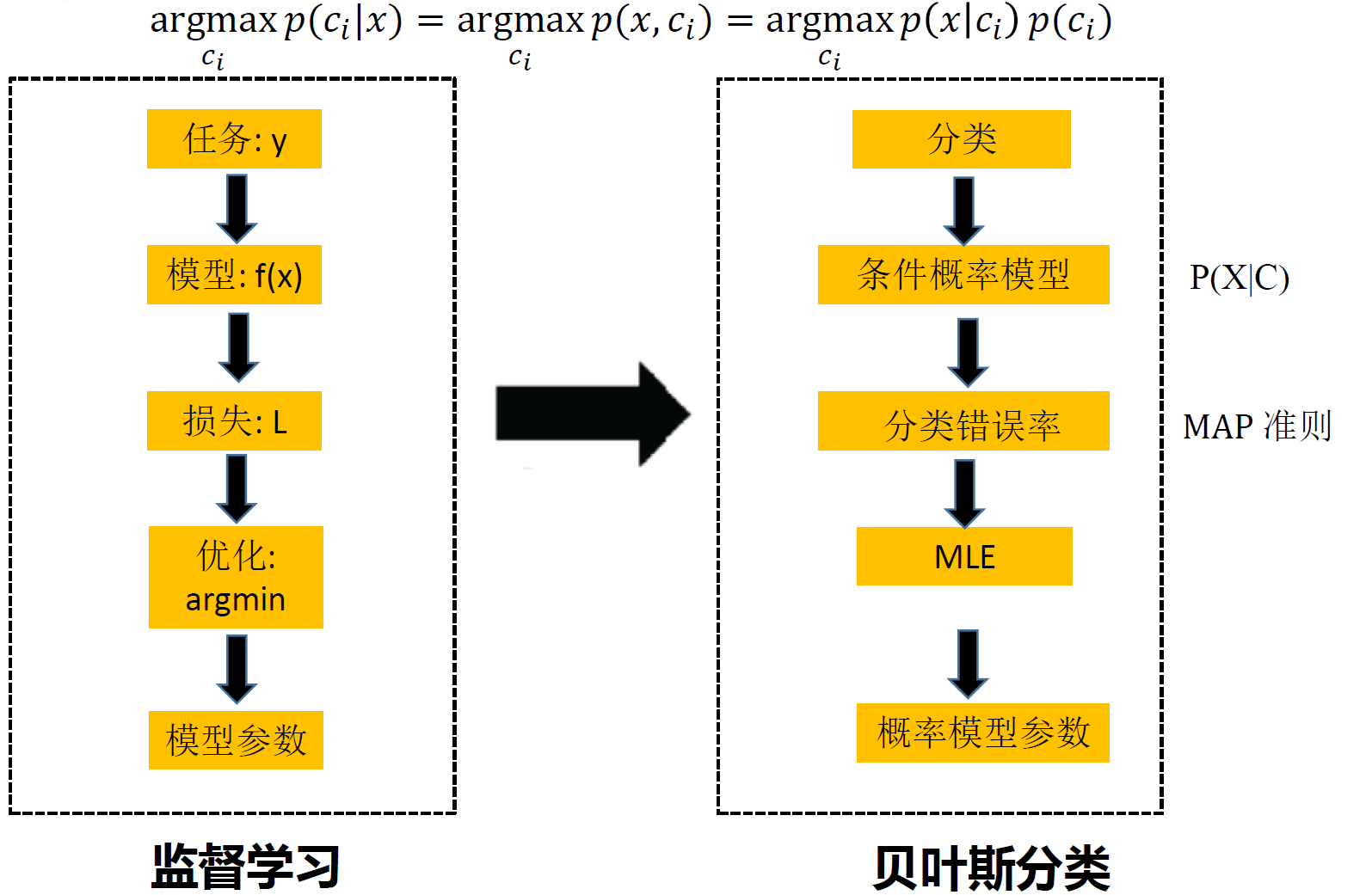
贝叶斯分类器



判别式模型:通过对 𝑃(𝑐|𝑥)直接建模预测,直接对条件概率建模,不关心背后的数据分布 𝑃(𝑥,𝑐)

生成式模型:概率分布建模


朴素贝叶斯分类器


避免0概率问题

朴素必要性

高斯朴素贝叶斯分类器
高斯分布
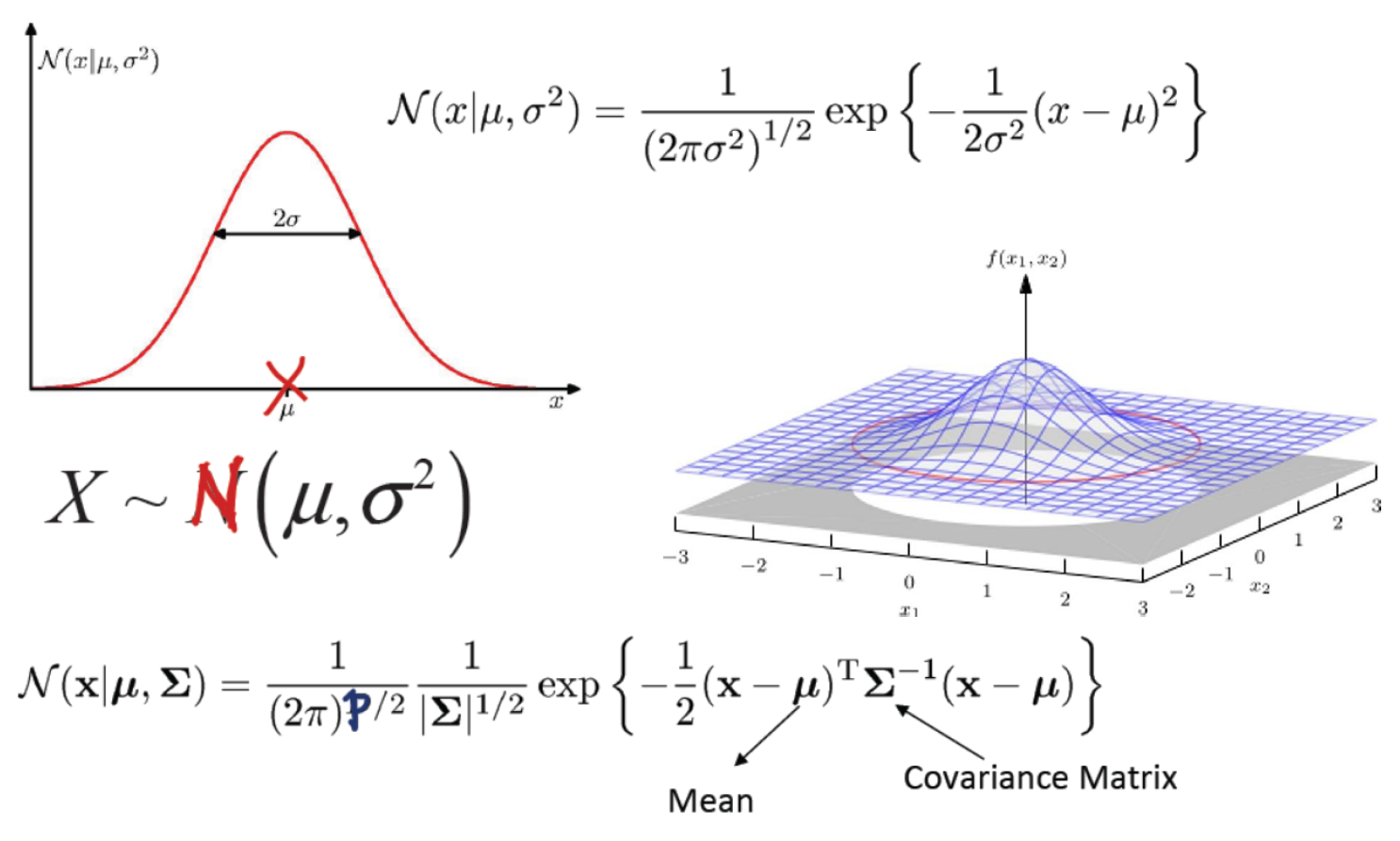
这里公式里的p是维度,即p维高斯
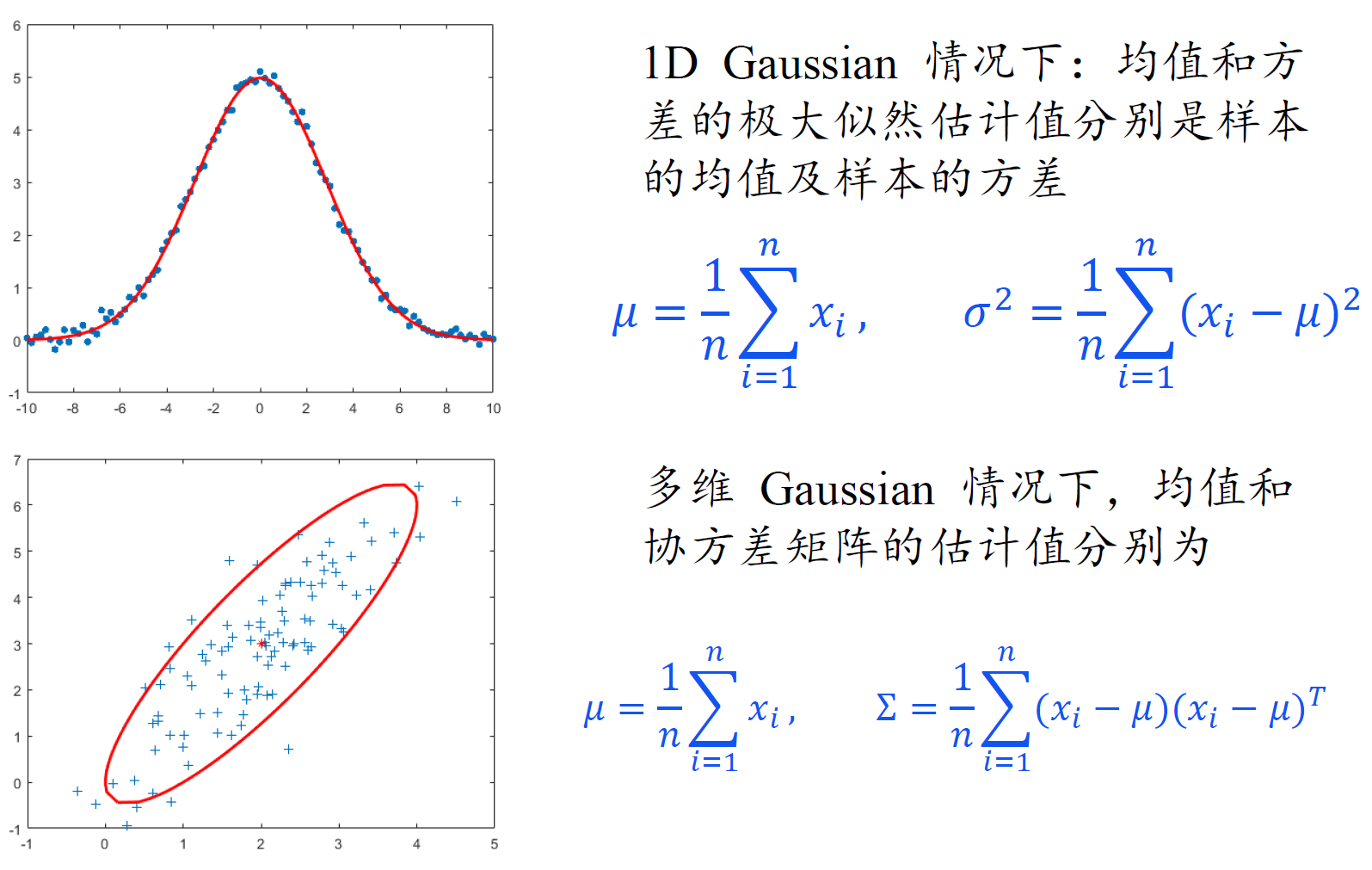
高斯朴素贝叶斯


朴素高斯必要性

高斯贝叶斯决策面

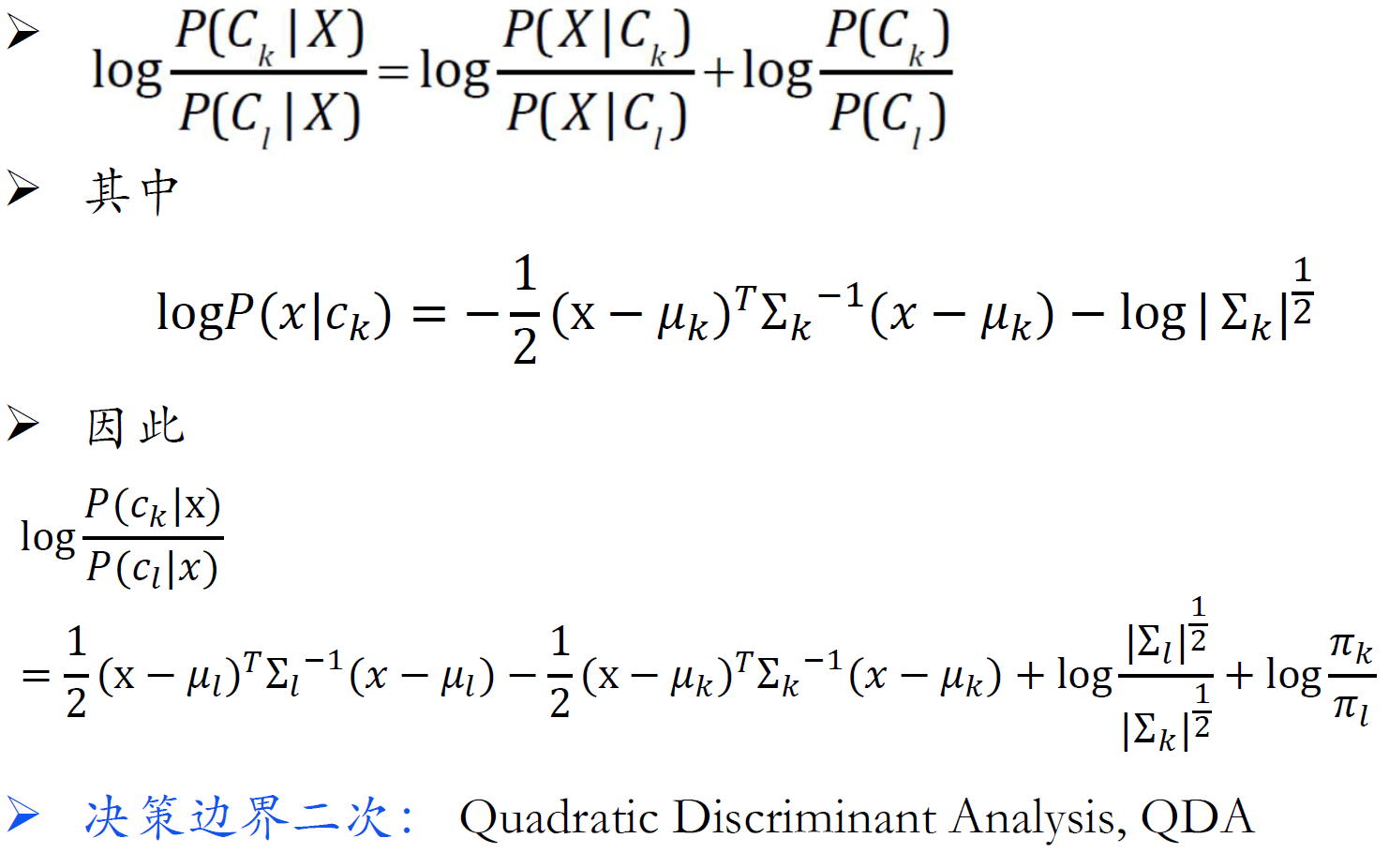
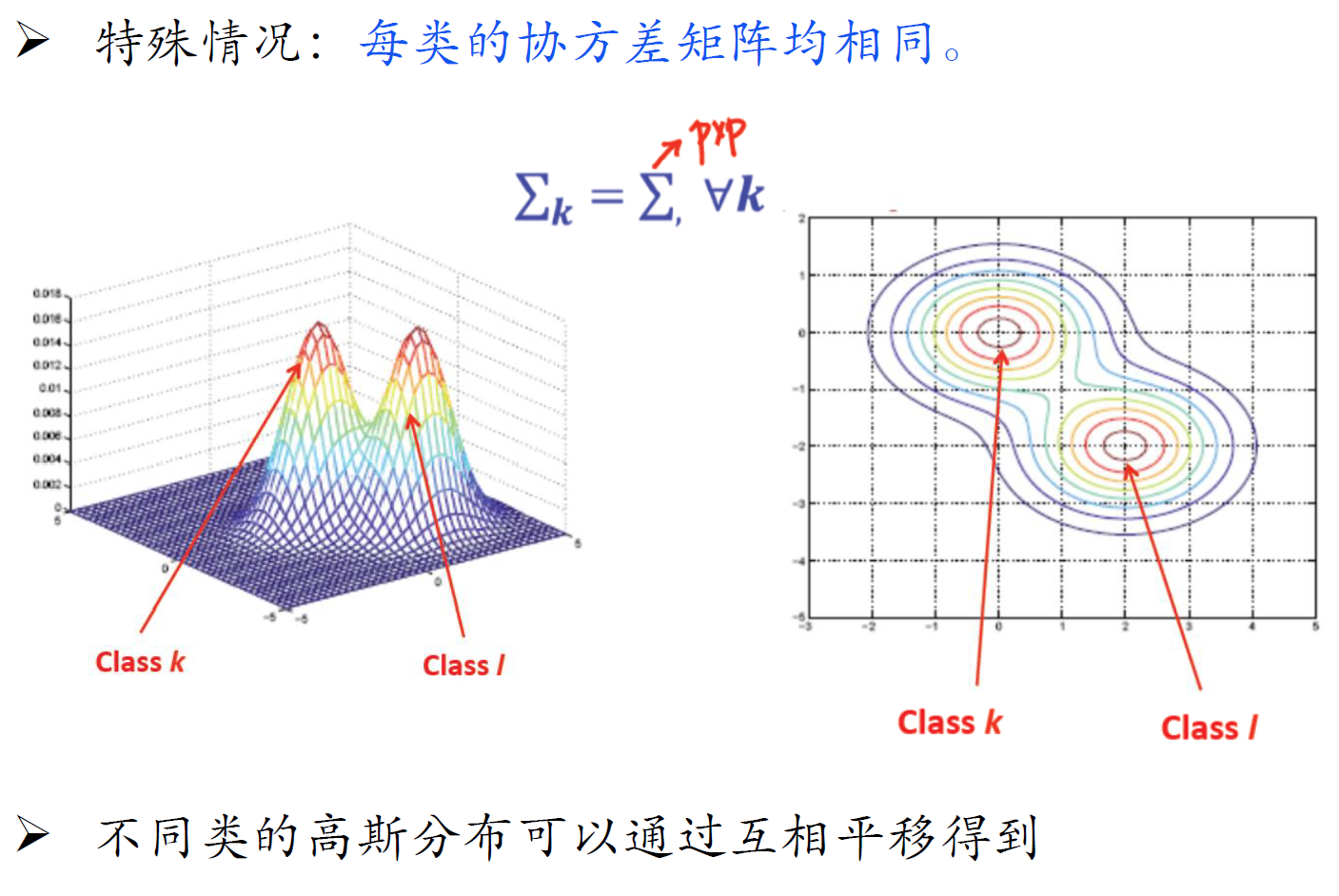

线性判别分析(LDA)
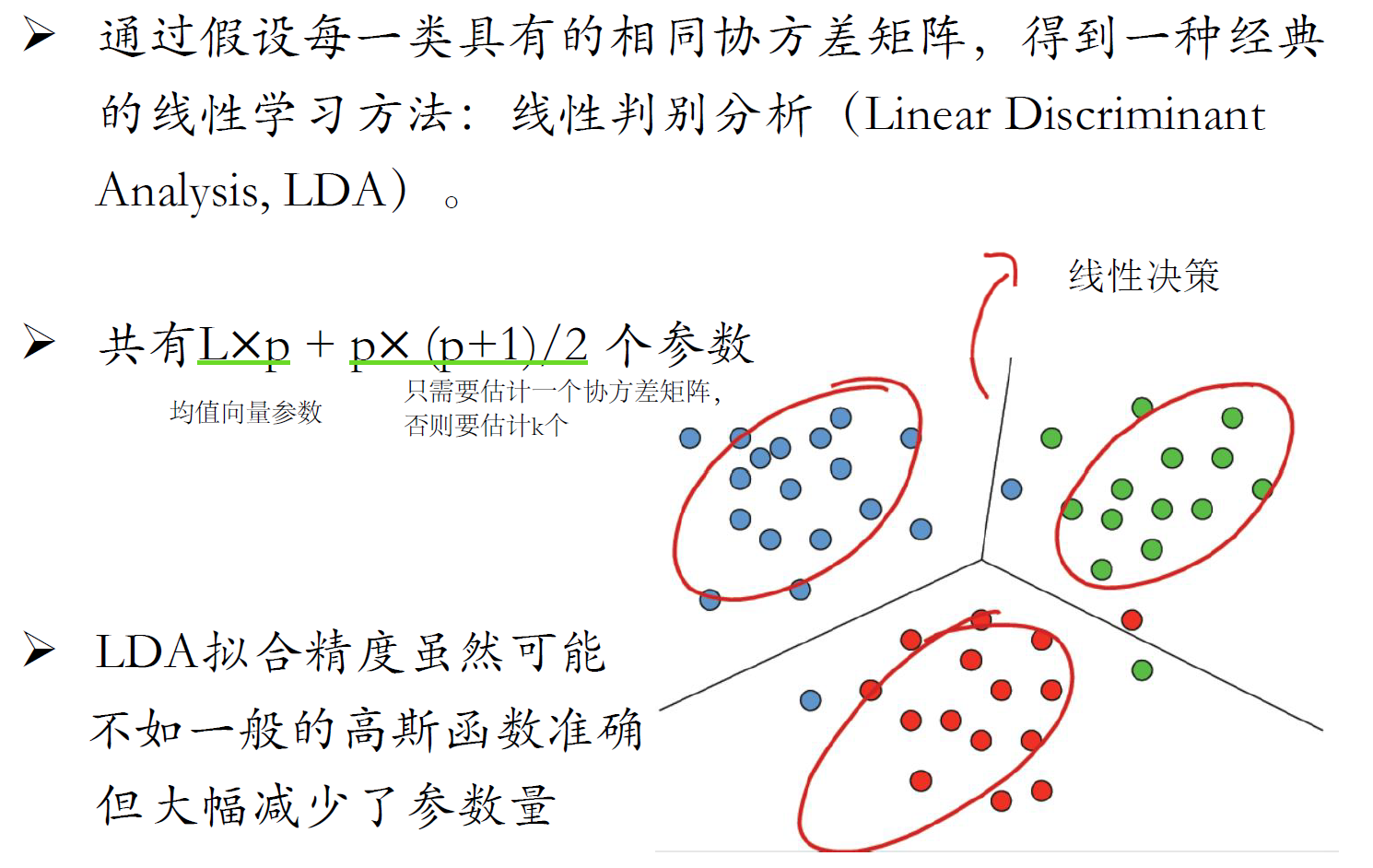

- LDA是假设协方差矩阵相同,朴素高斯和非朴素高斯的区别在于协方差矩阵是否为对角阵
LDA vs 逻辑回归
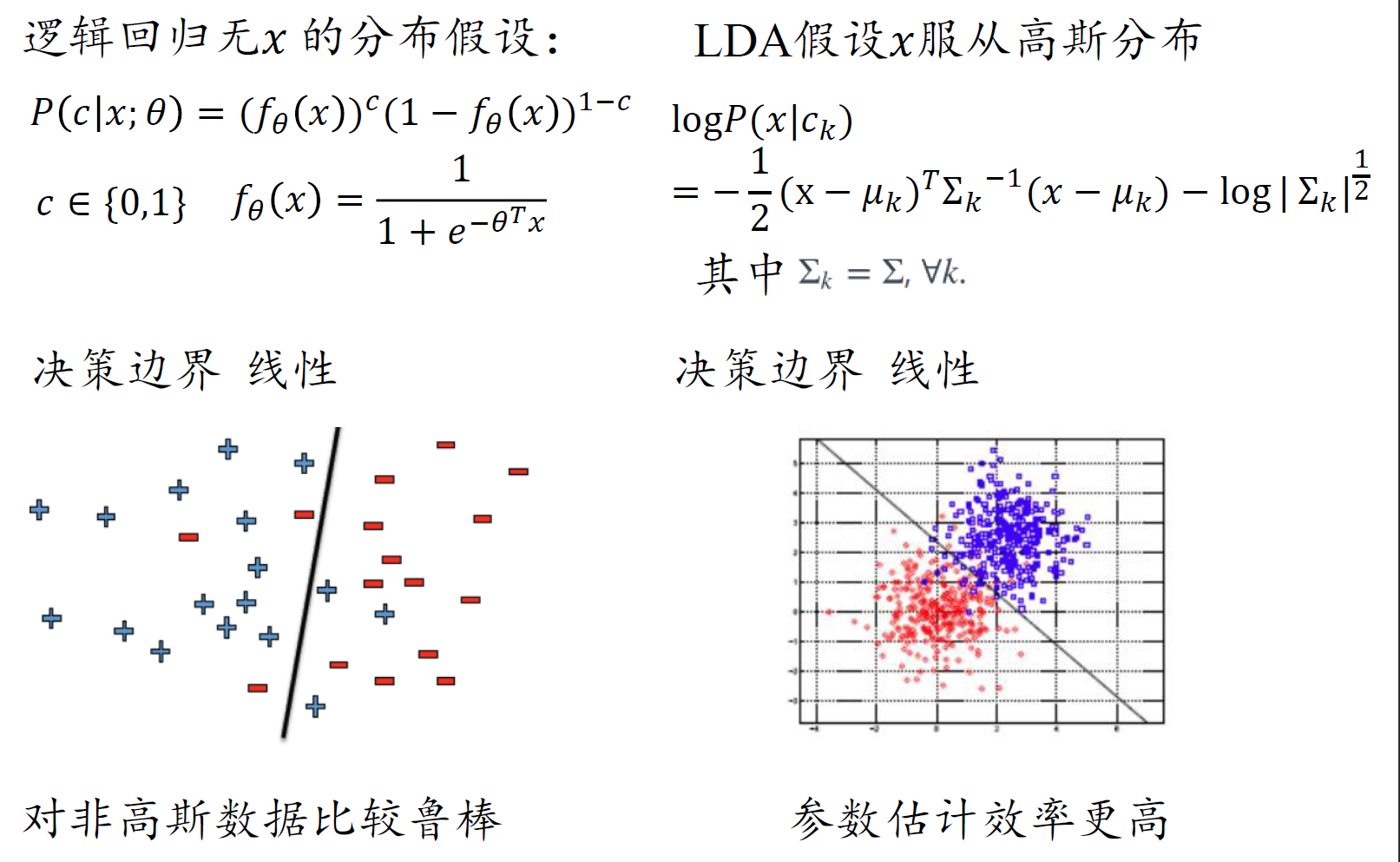
高斯朴素贝叶斯决策面

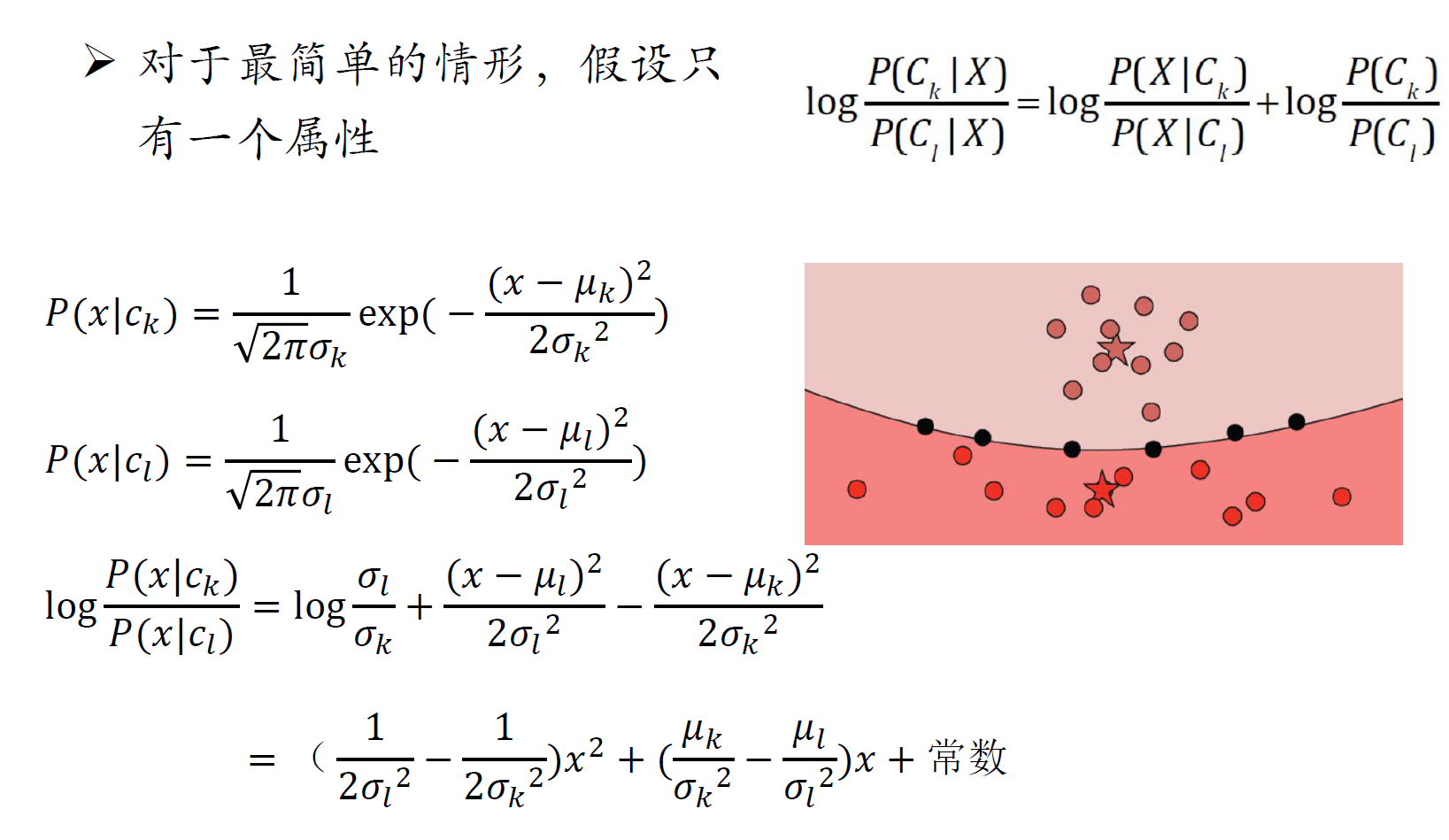
总结
- 朴素贝叶斯可以处理离散属性和可以处理连续属性

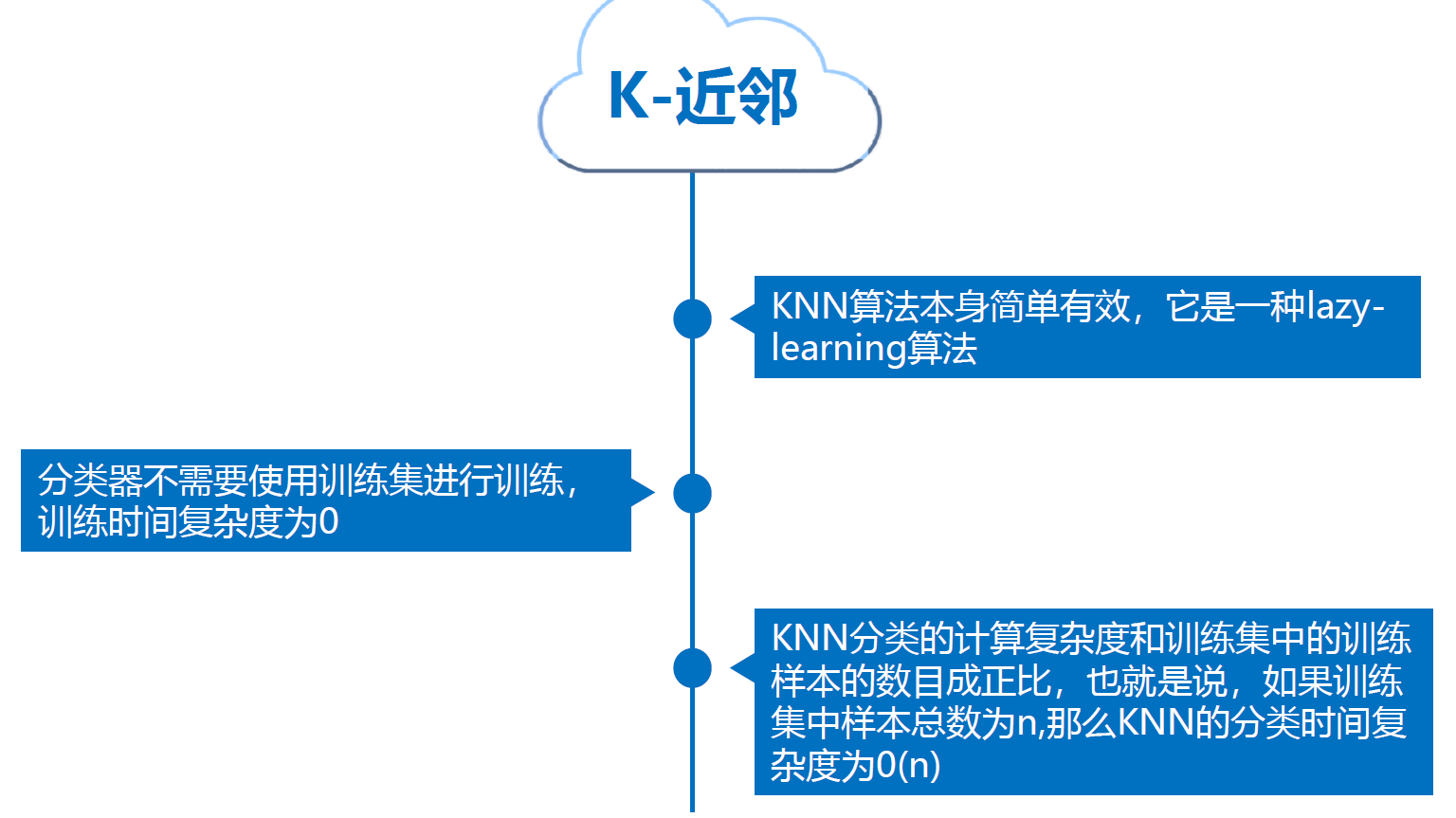
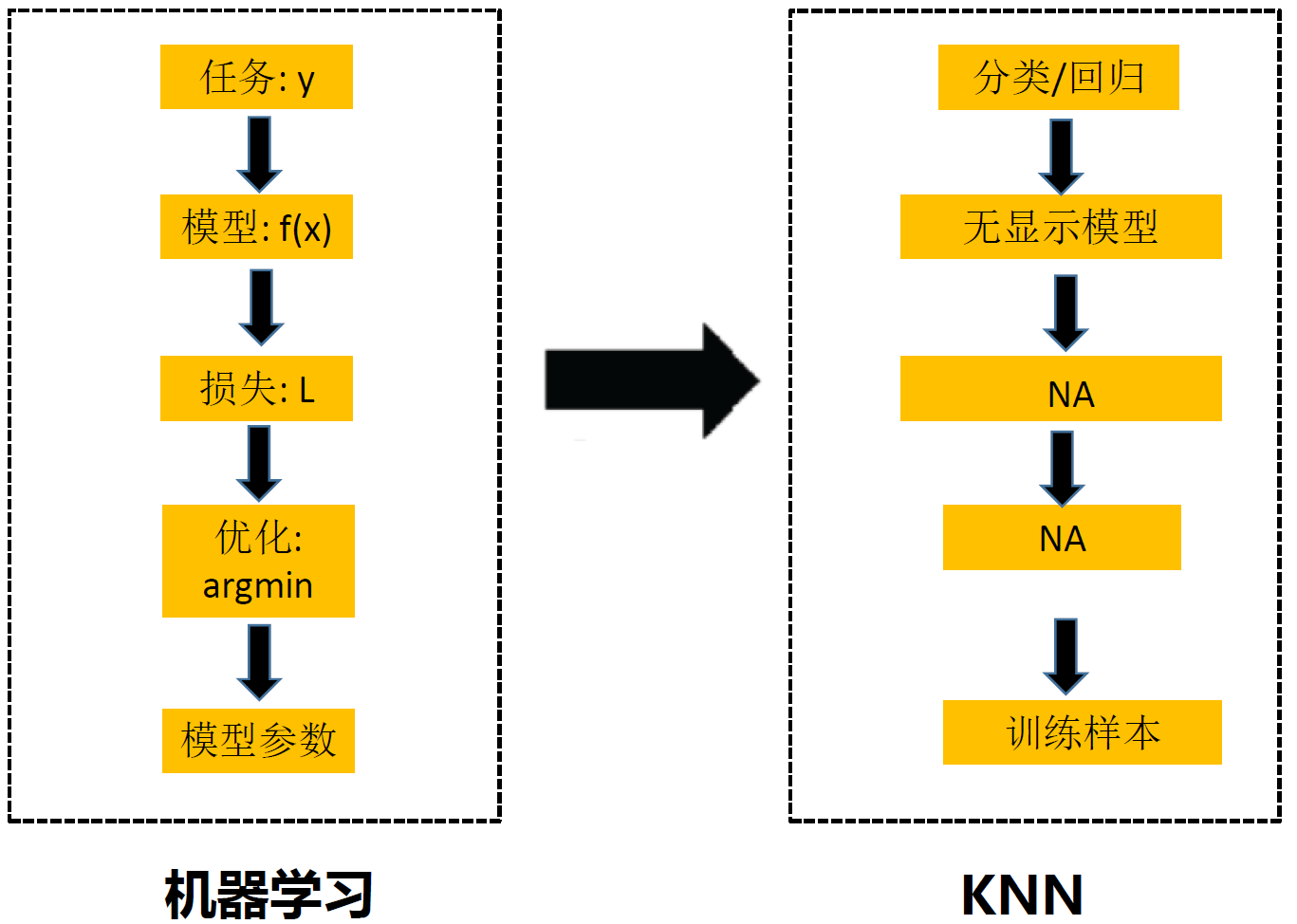
KNN
六、GMM、EM
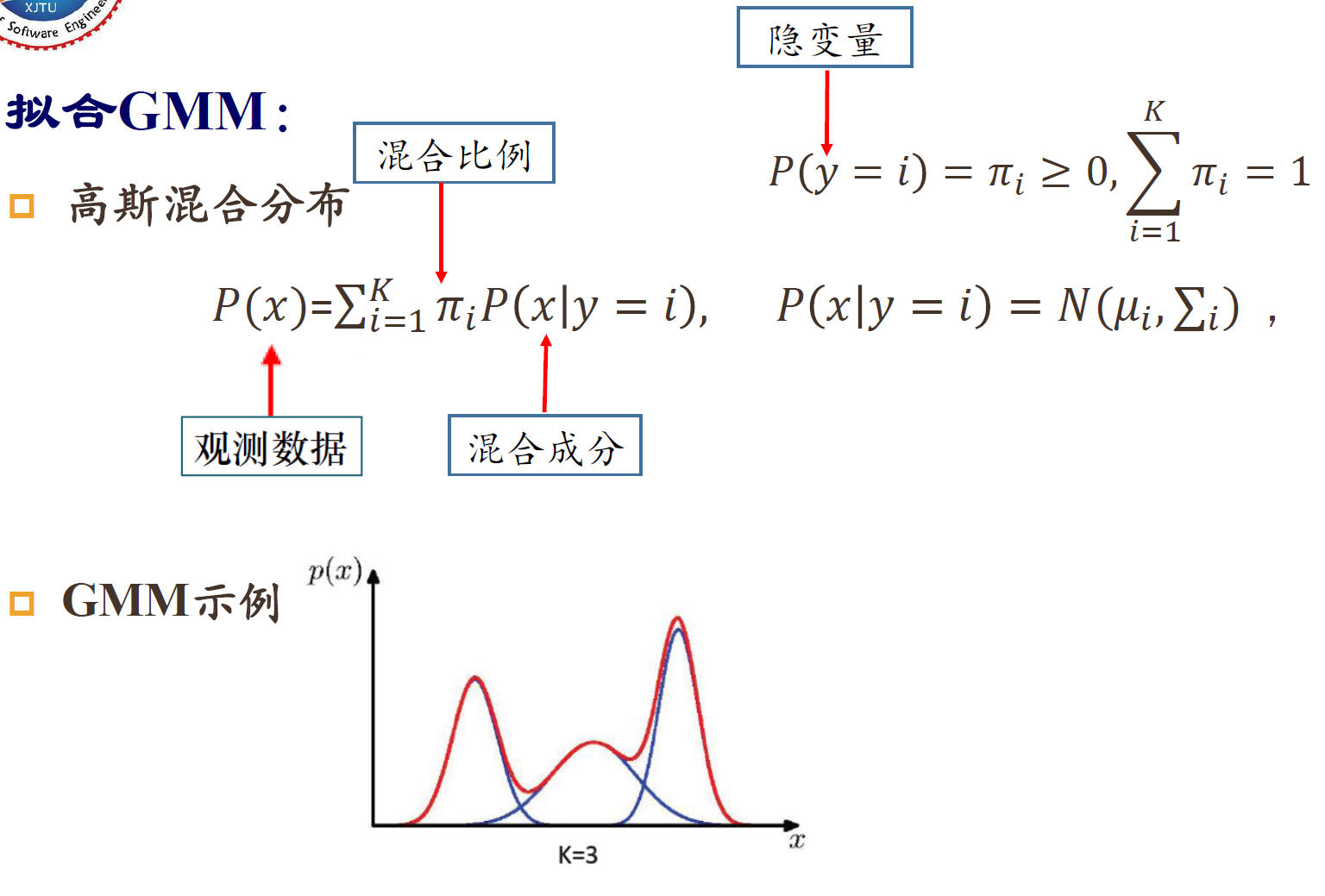
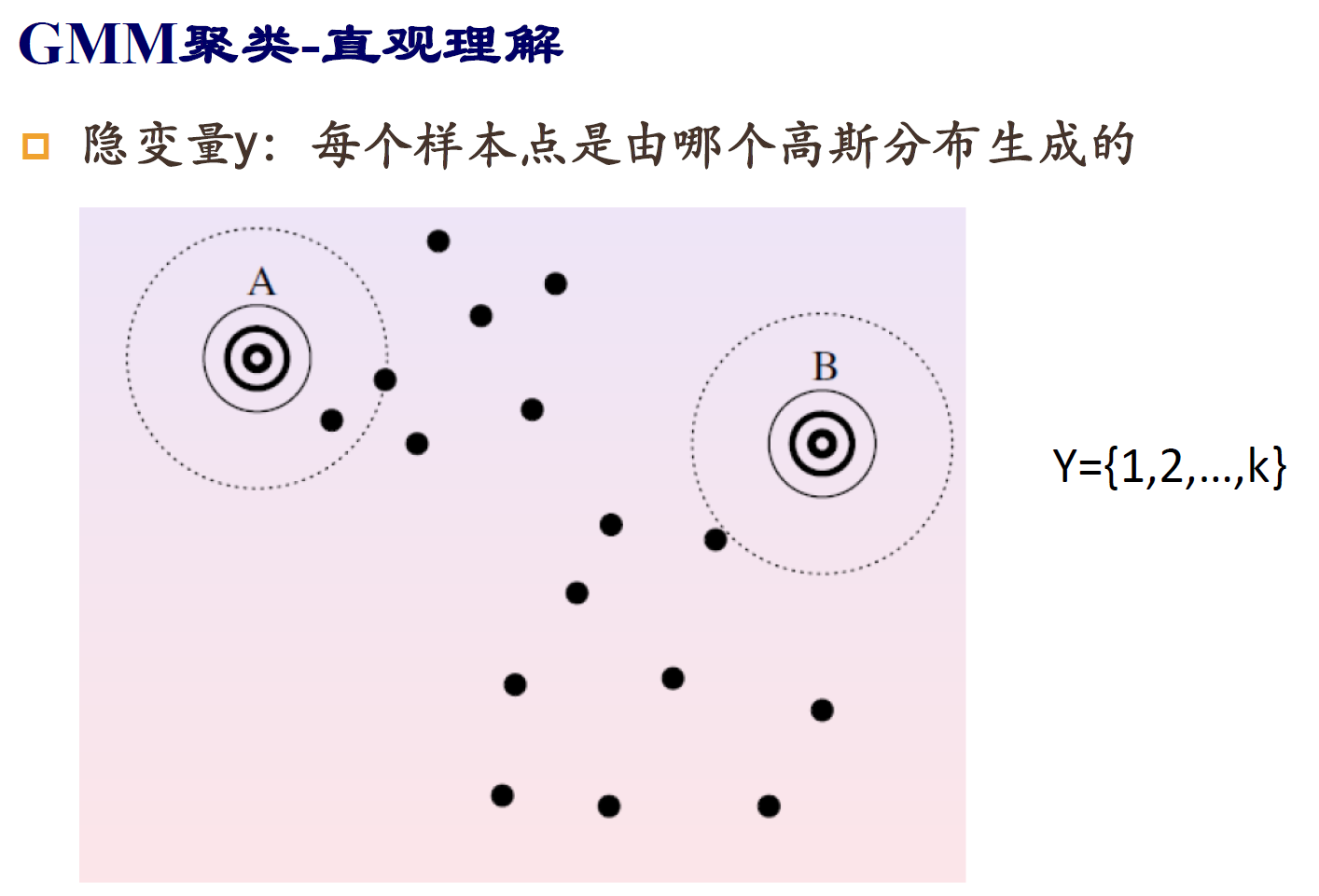
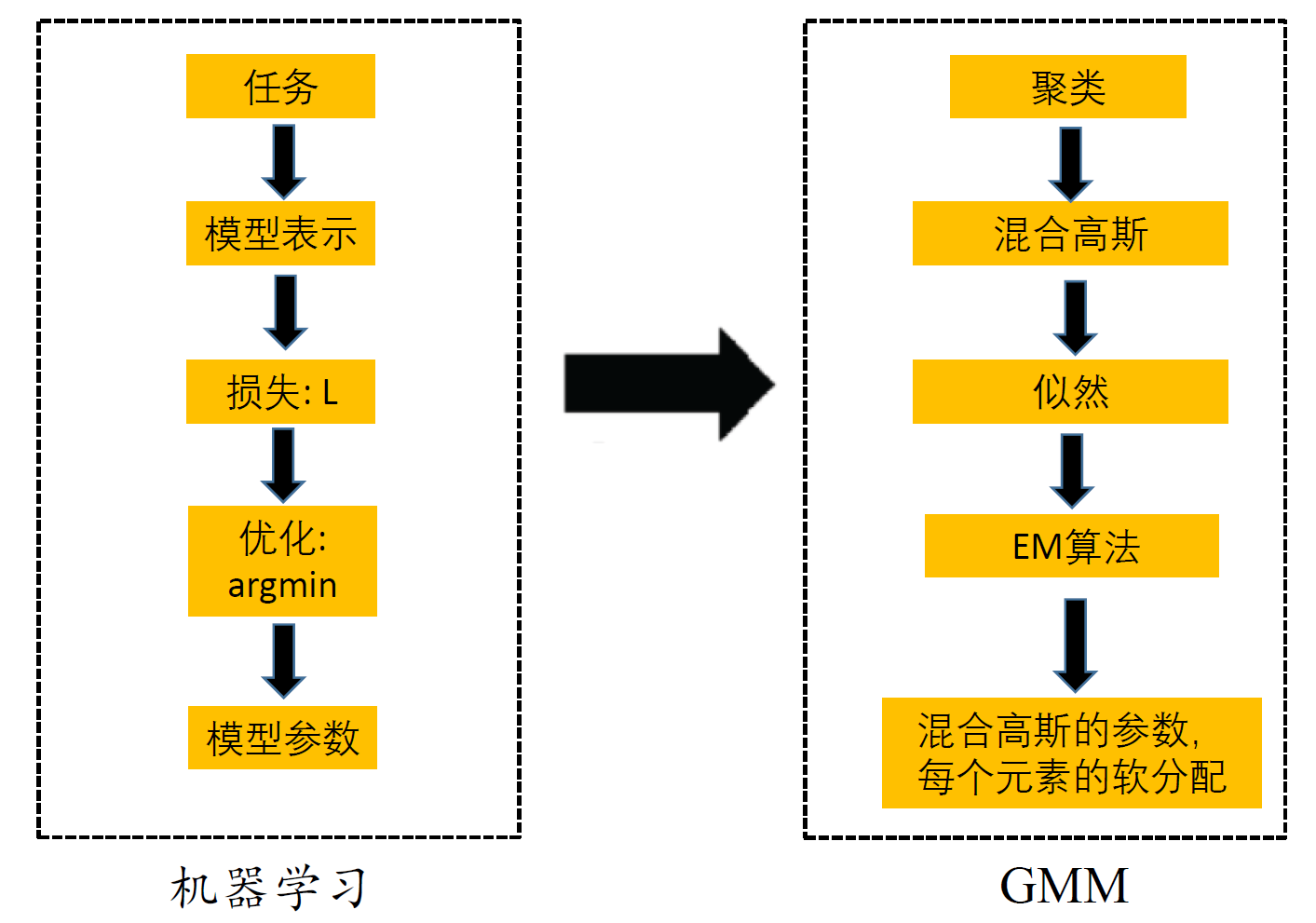
GMM



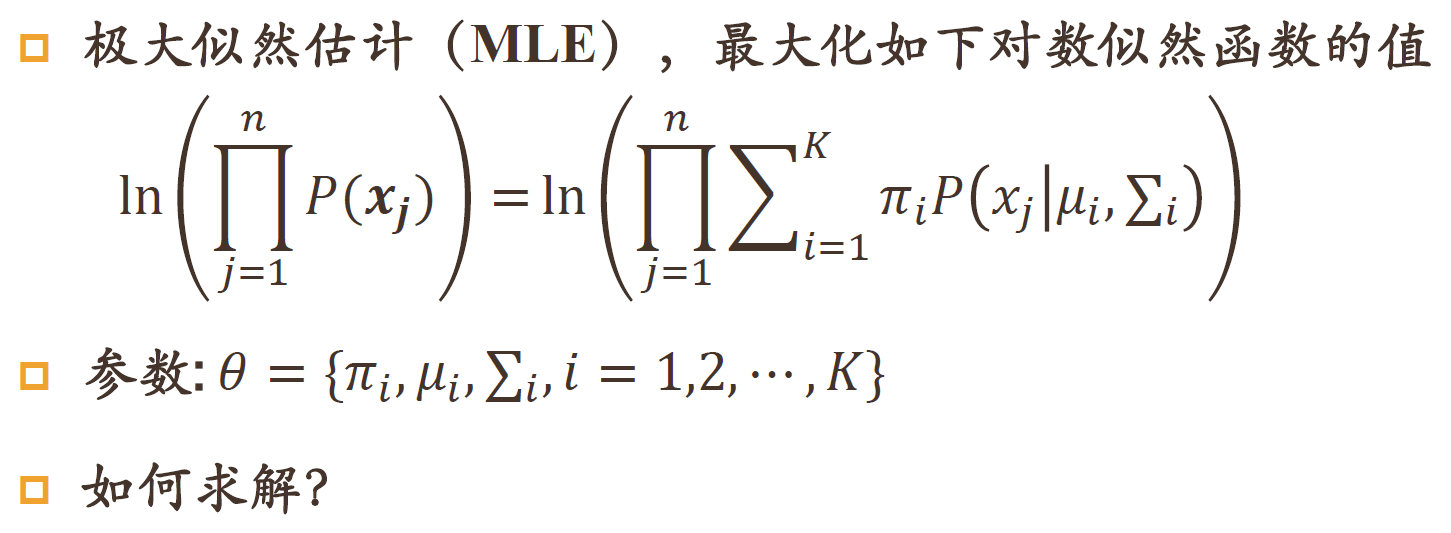
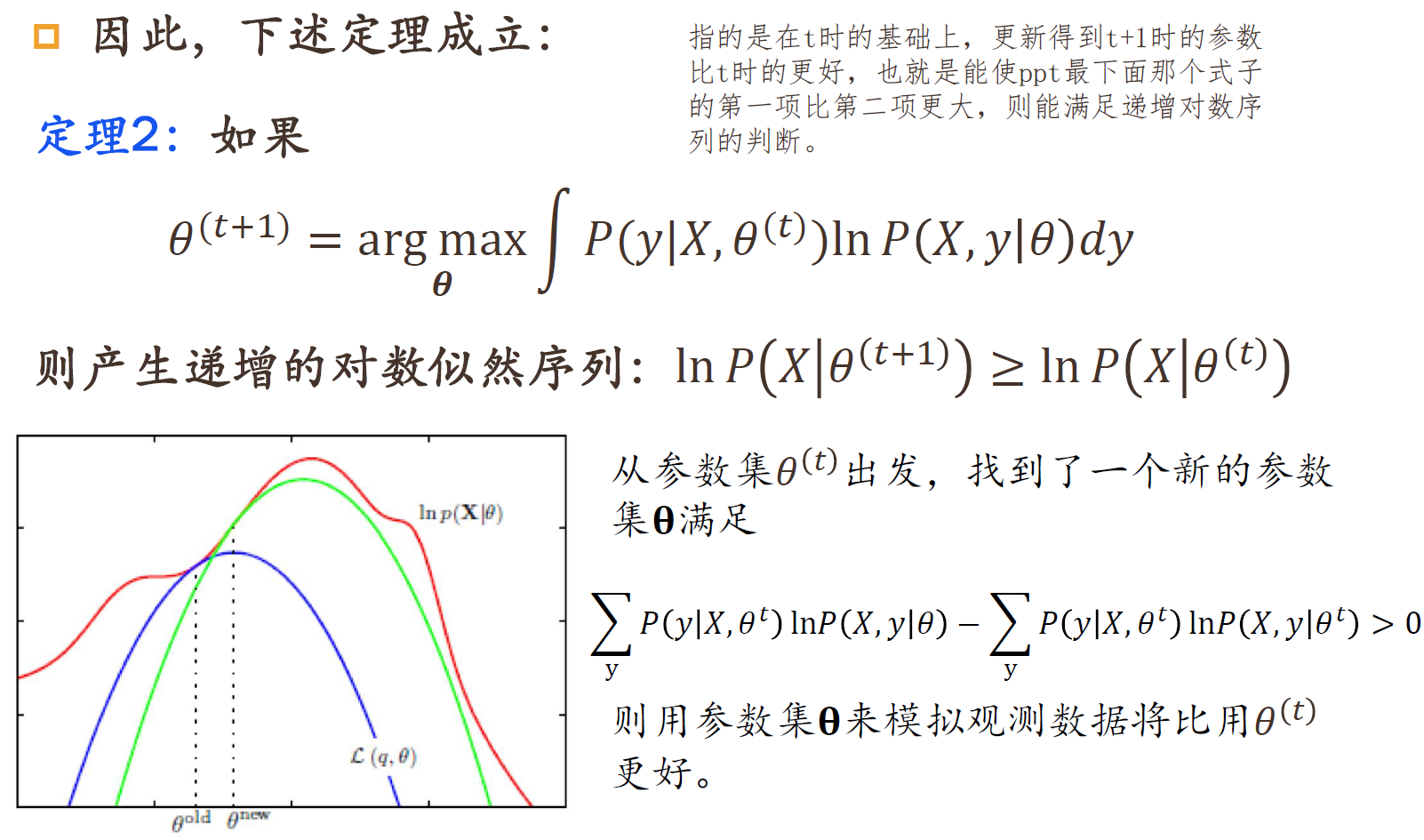
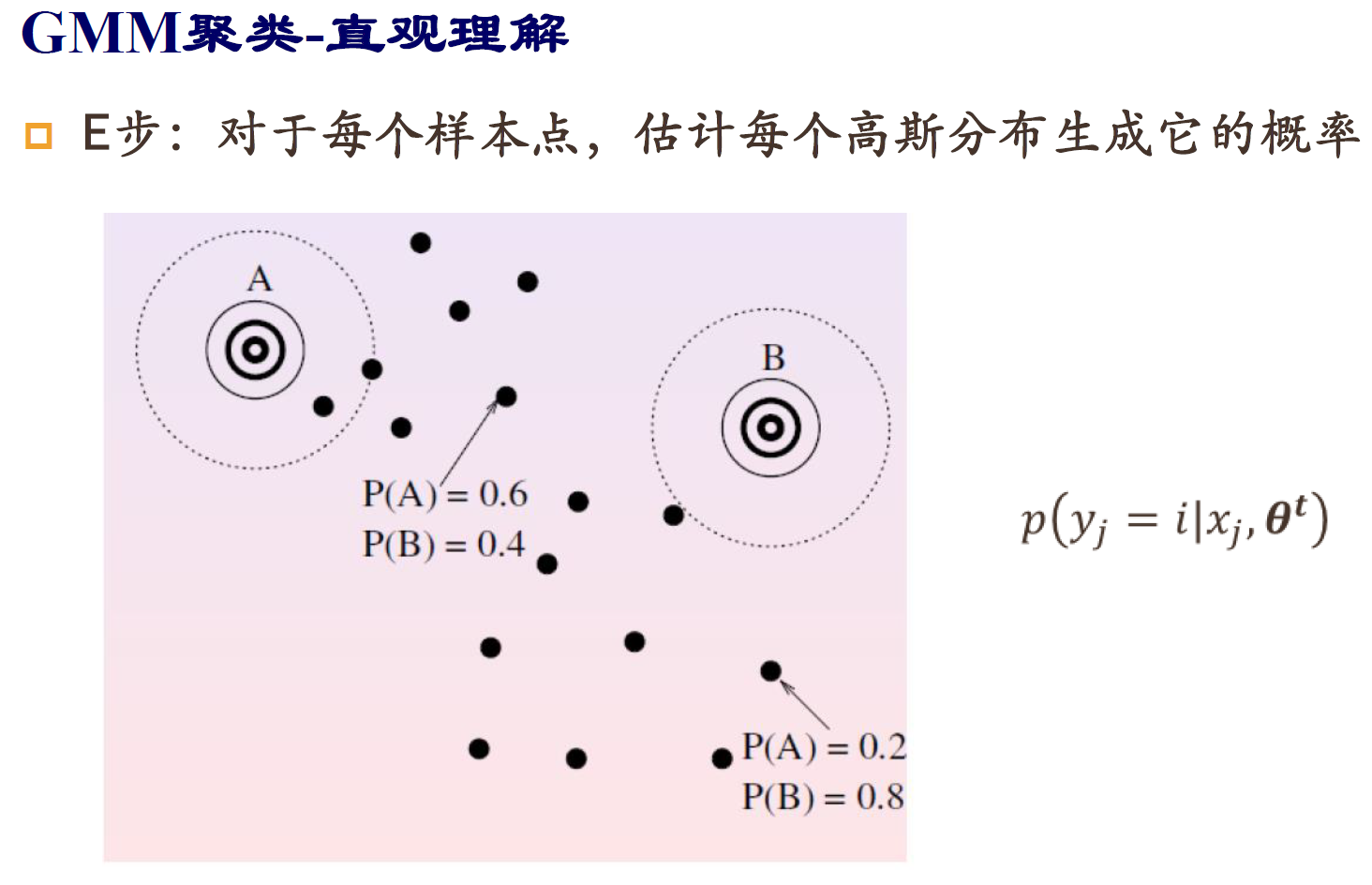
EM算法求解


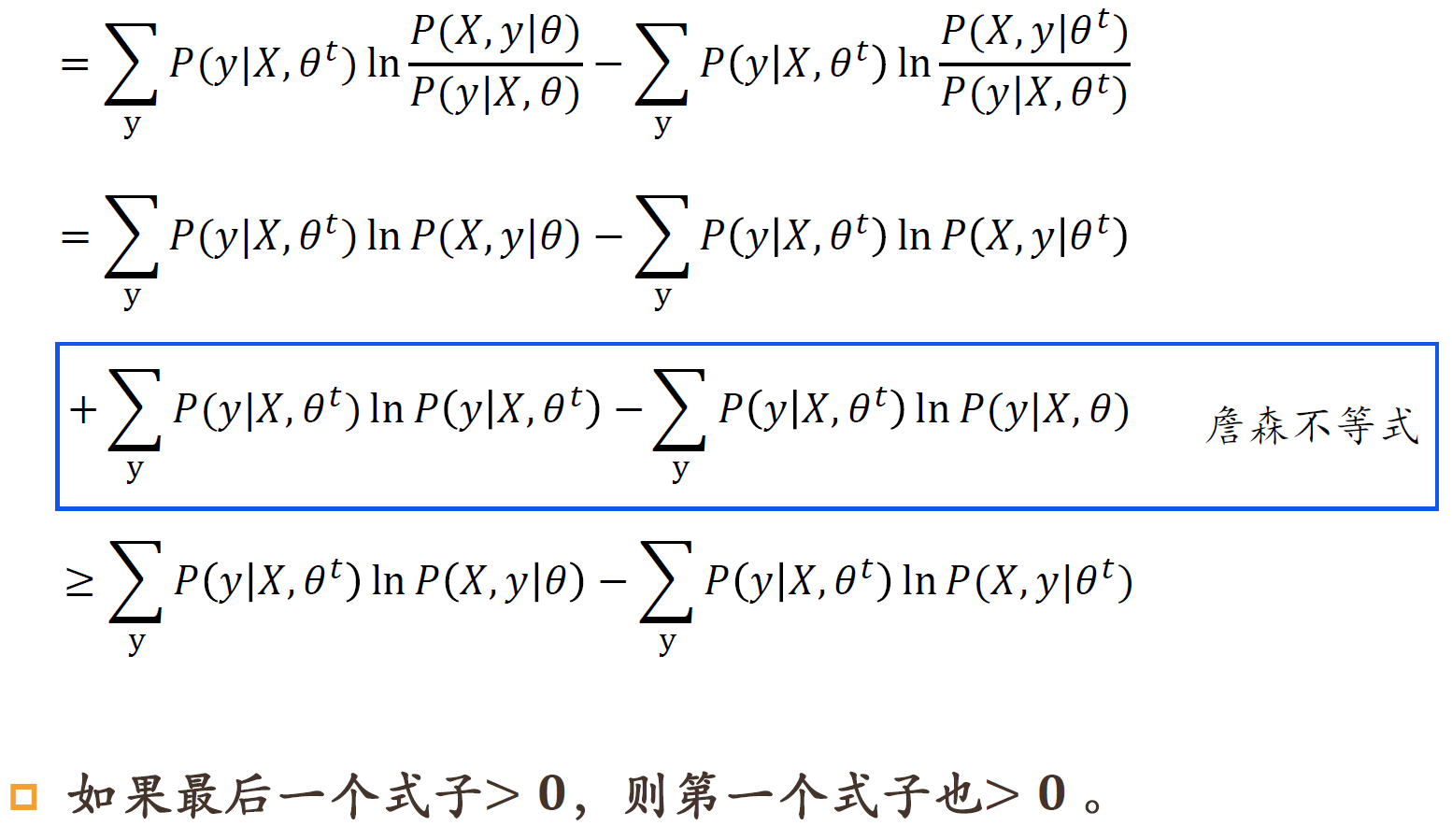





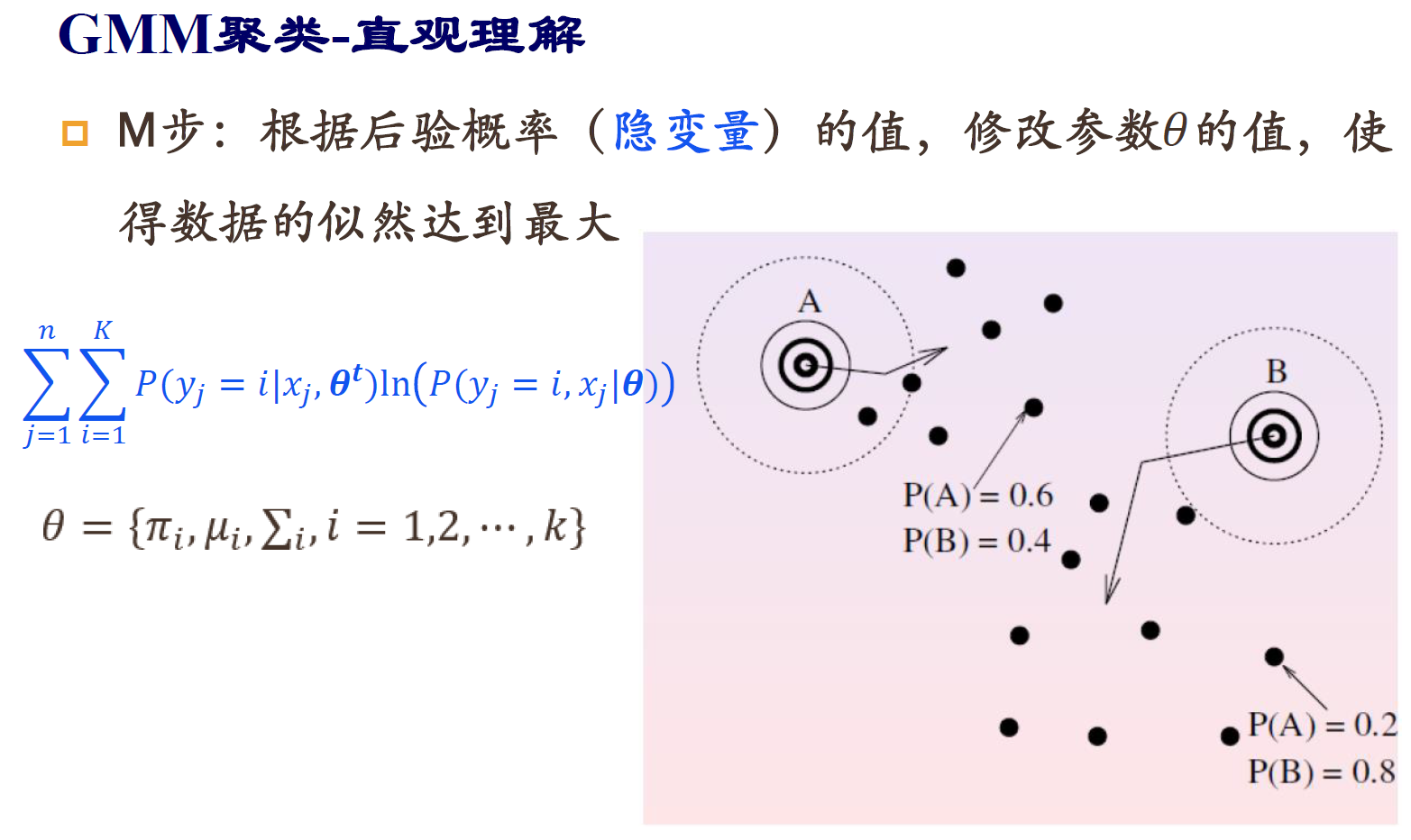
缺点
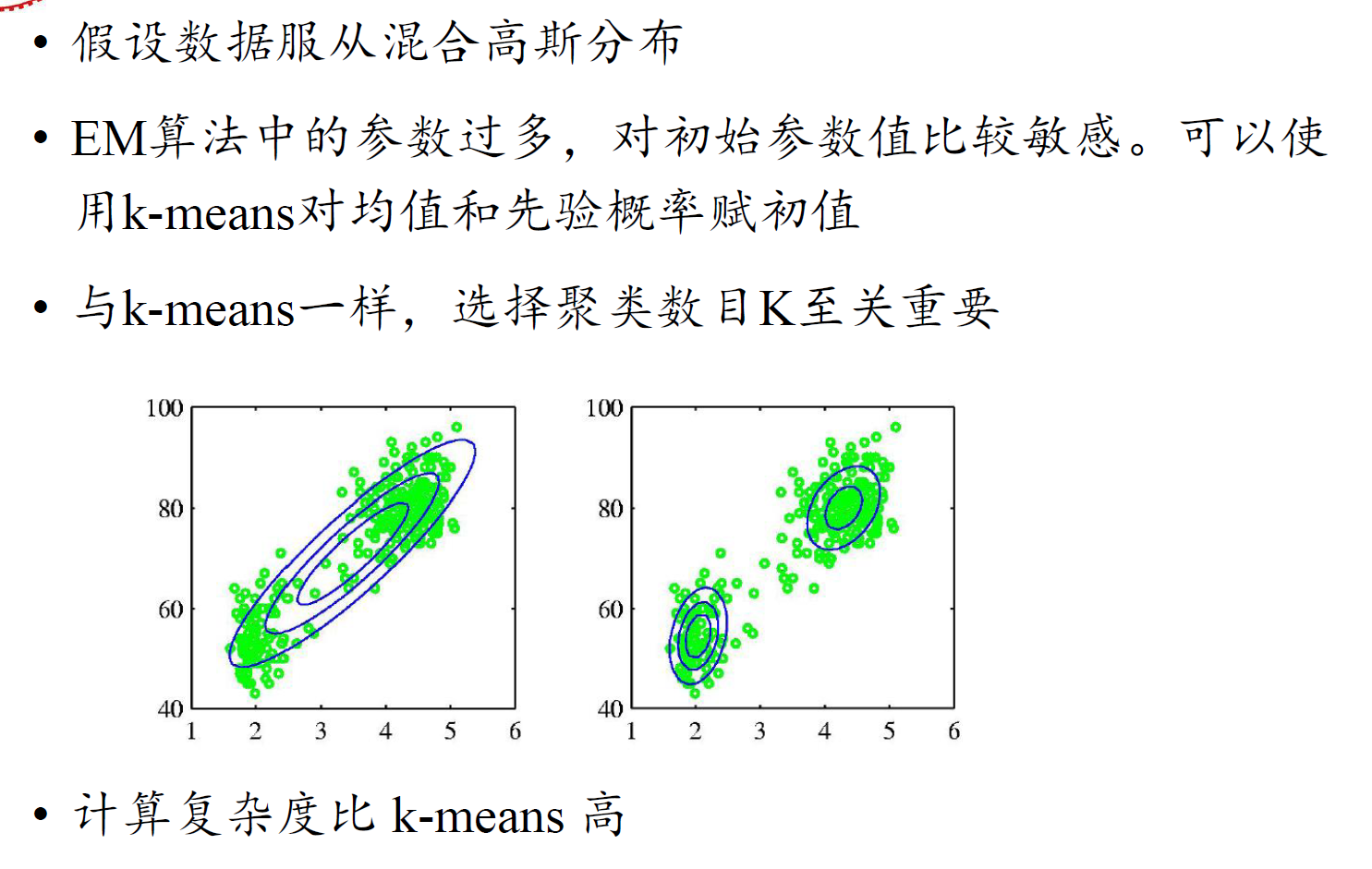
总结
七、马尔可夫链
贝叶斯网

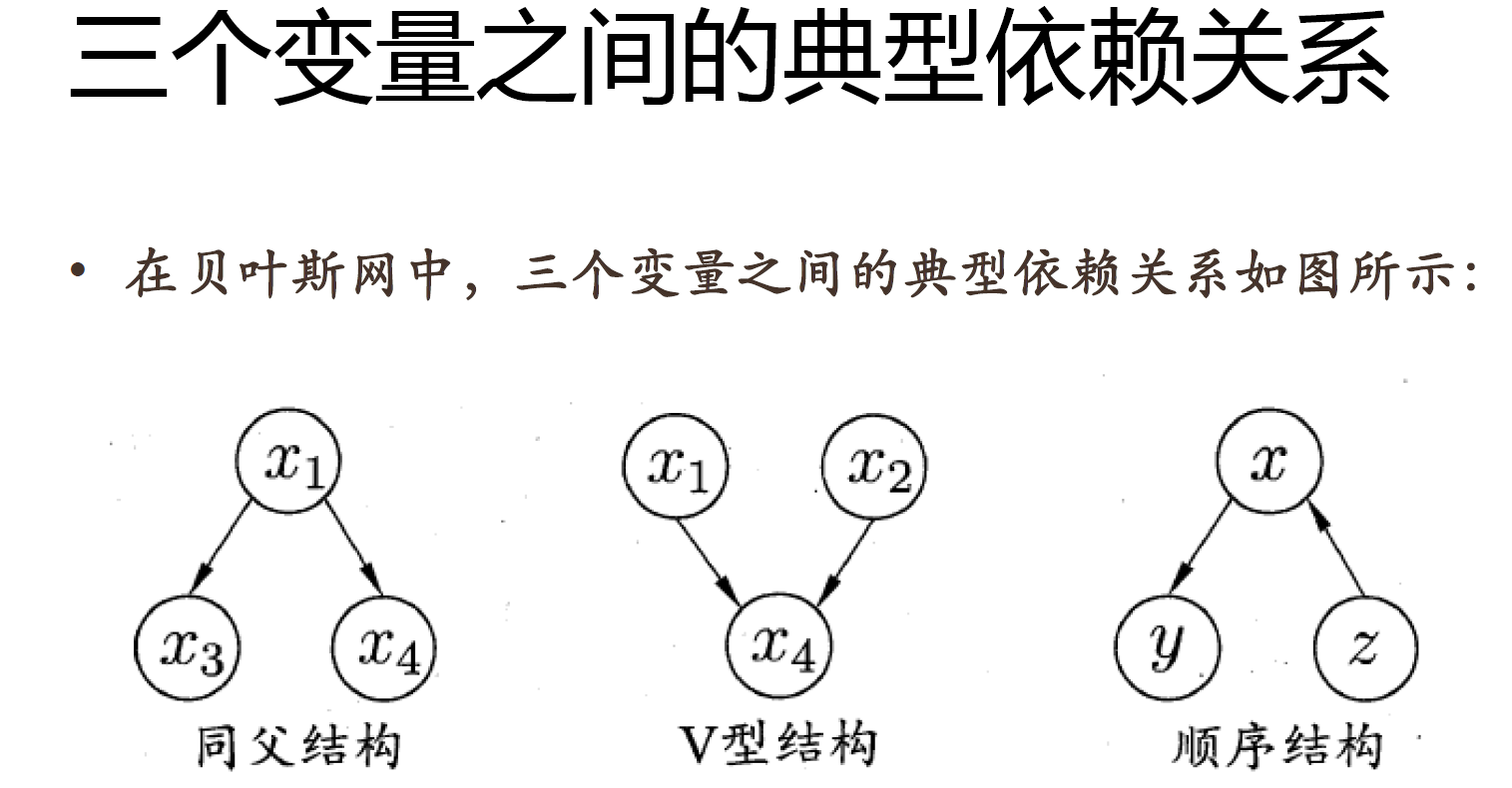


马尔可夫链


三要素

状态转移







八、PCA
http://blog.codinglabs.org/articles/pca-tutorial.html

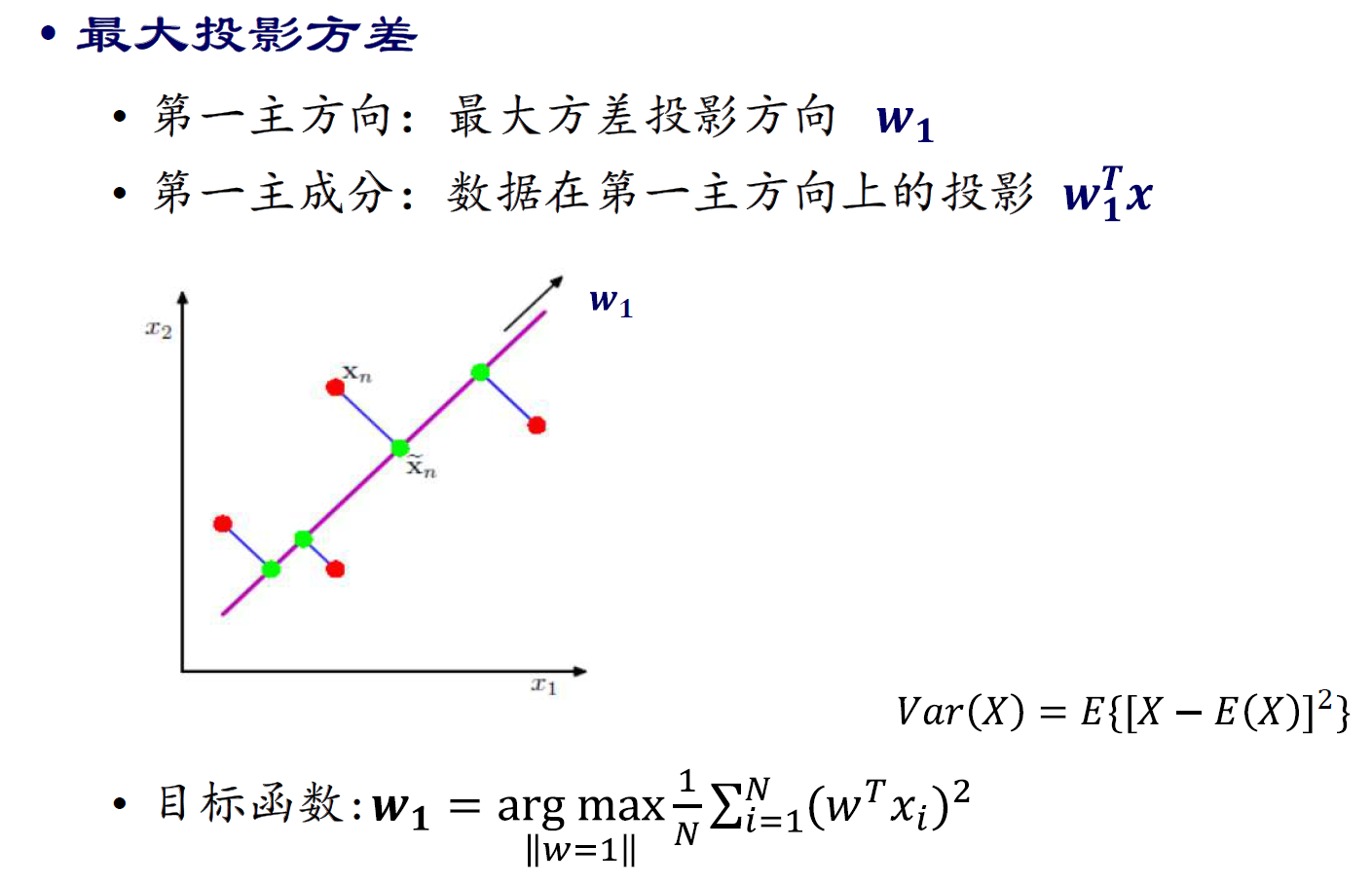




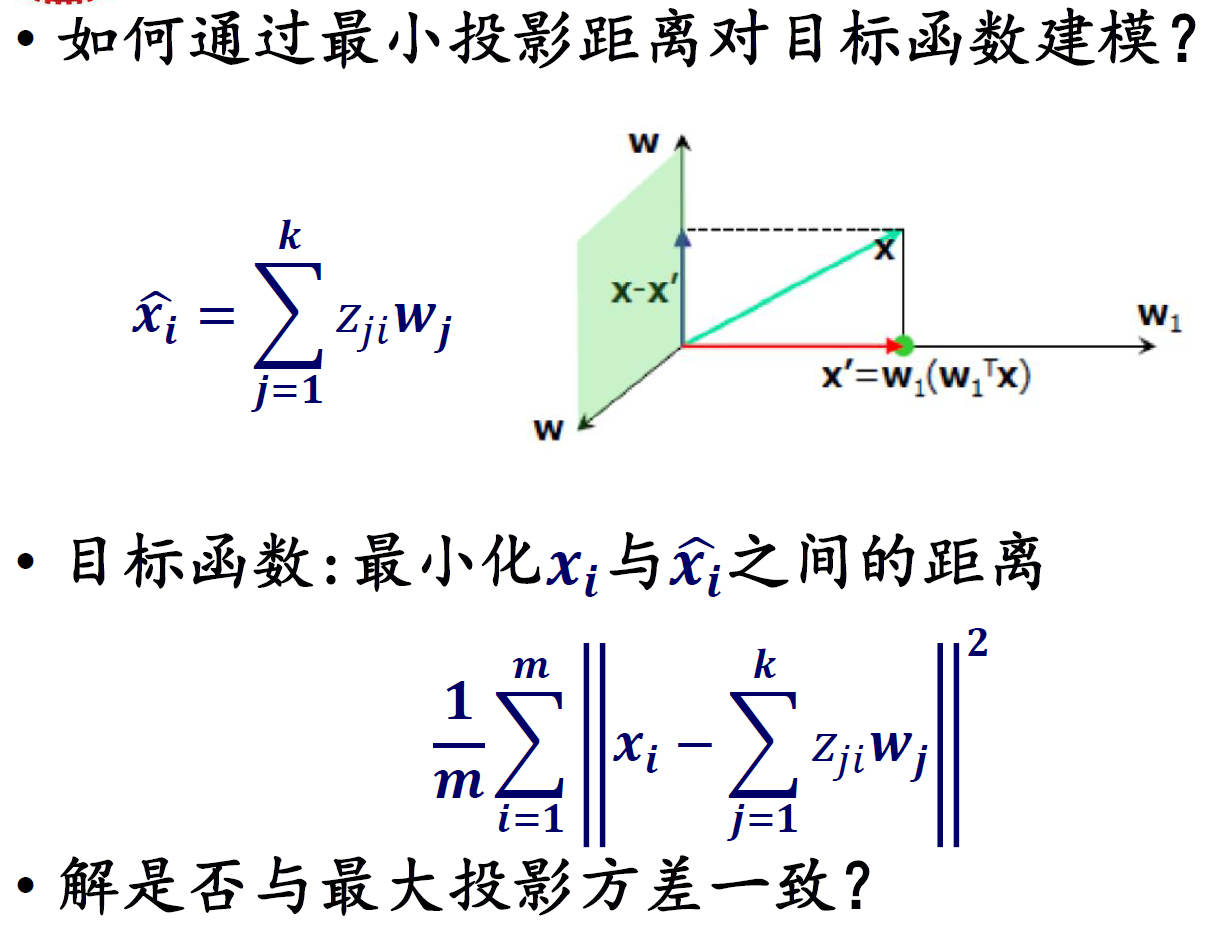

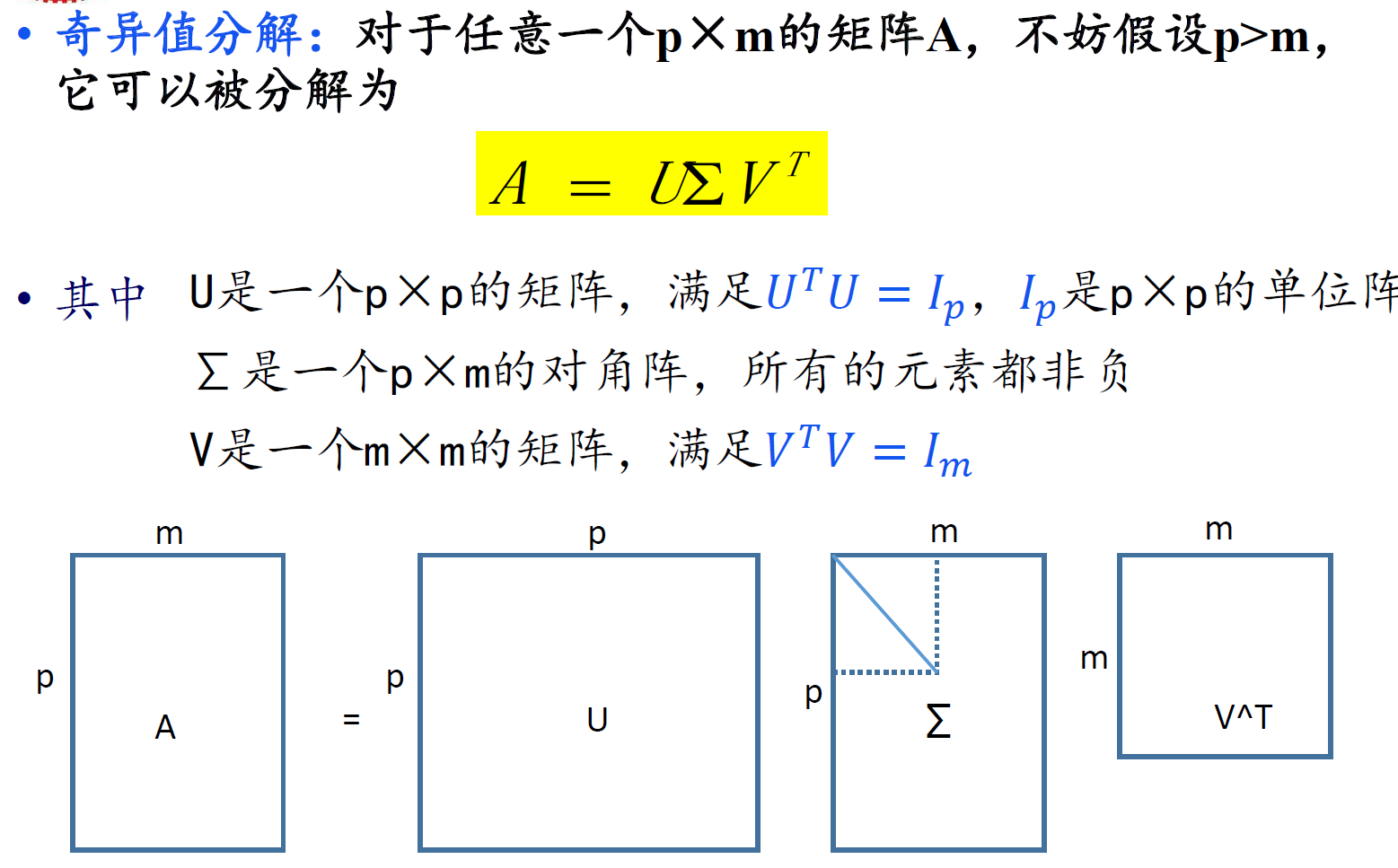
SVD

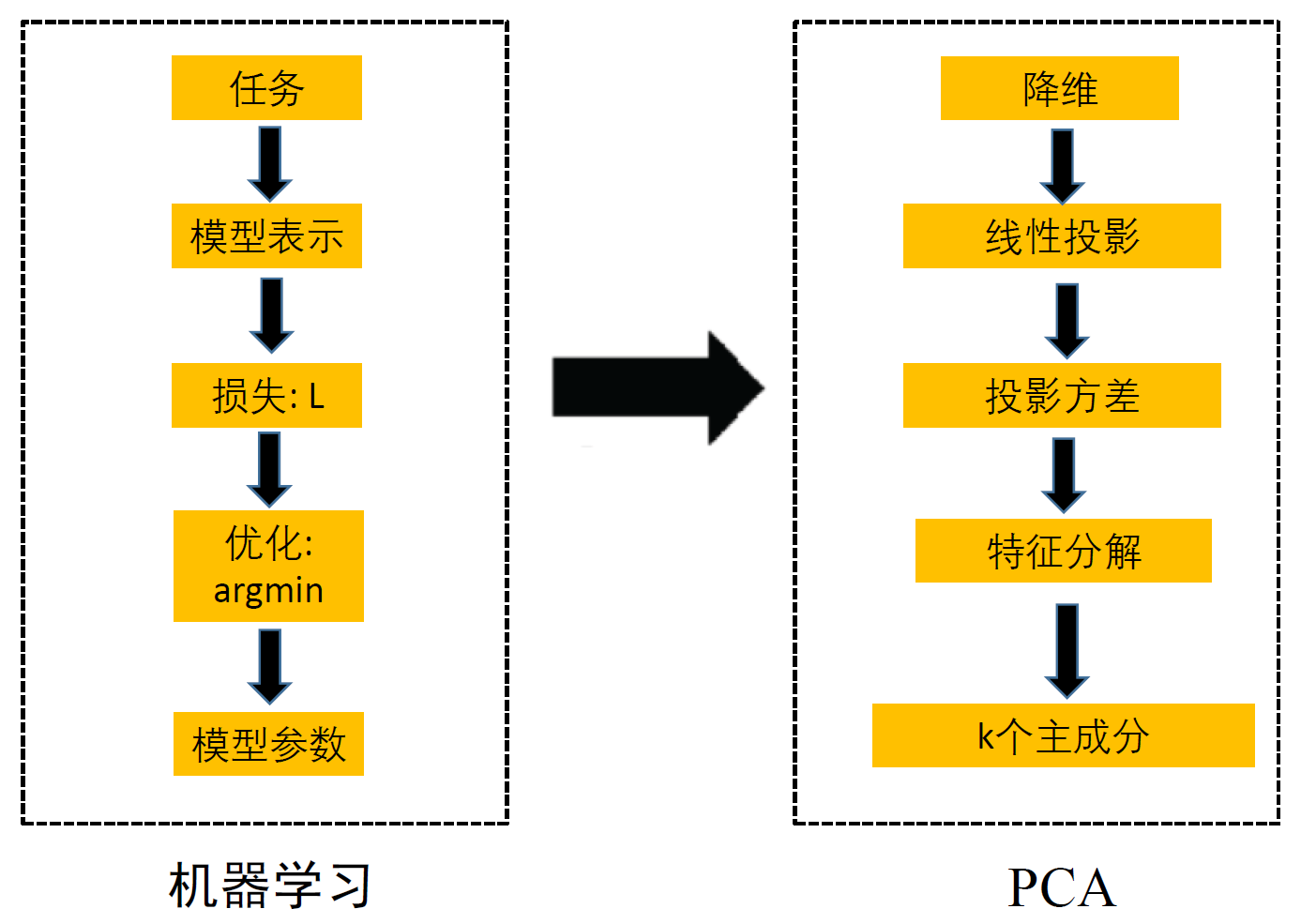
方法

概率PCA











PCA EM算法

核PCA

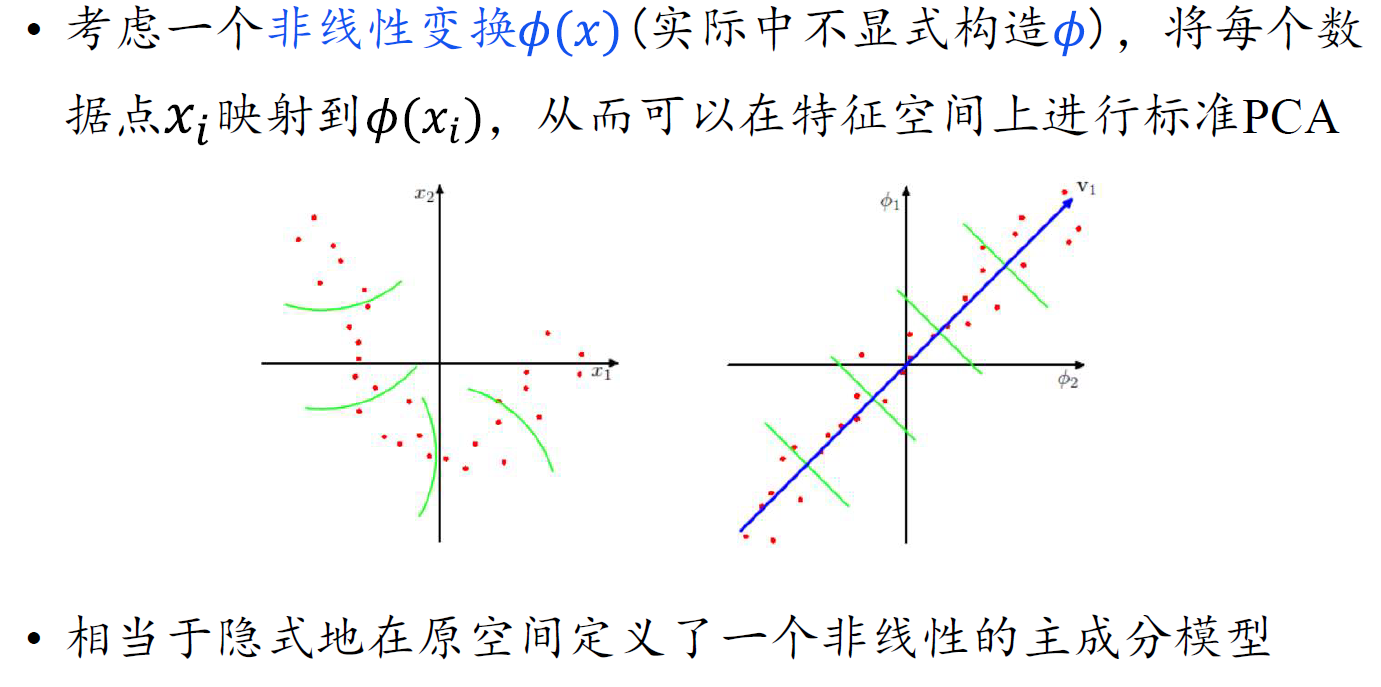

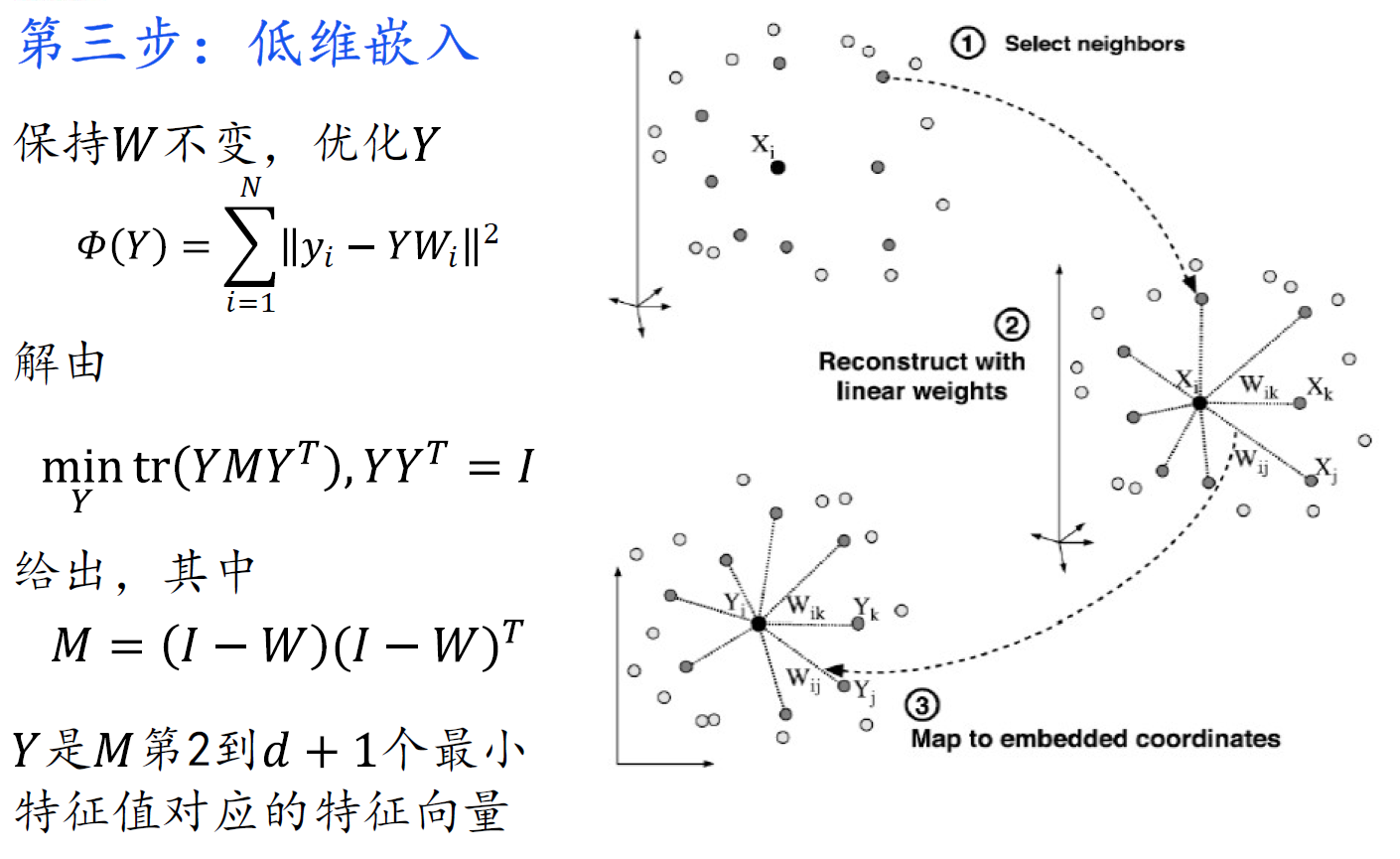
LLE

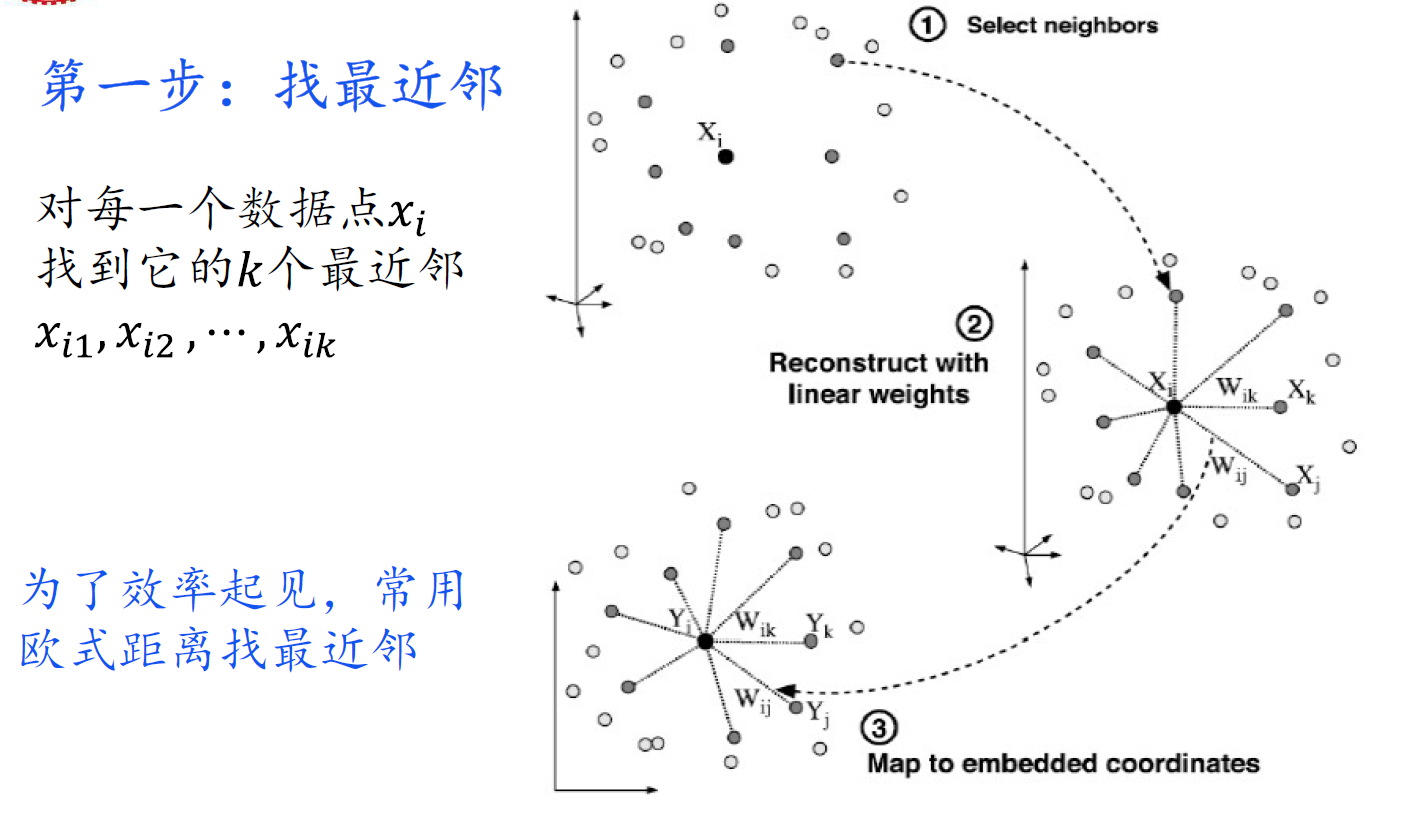
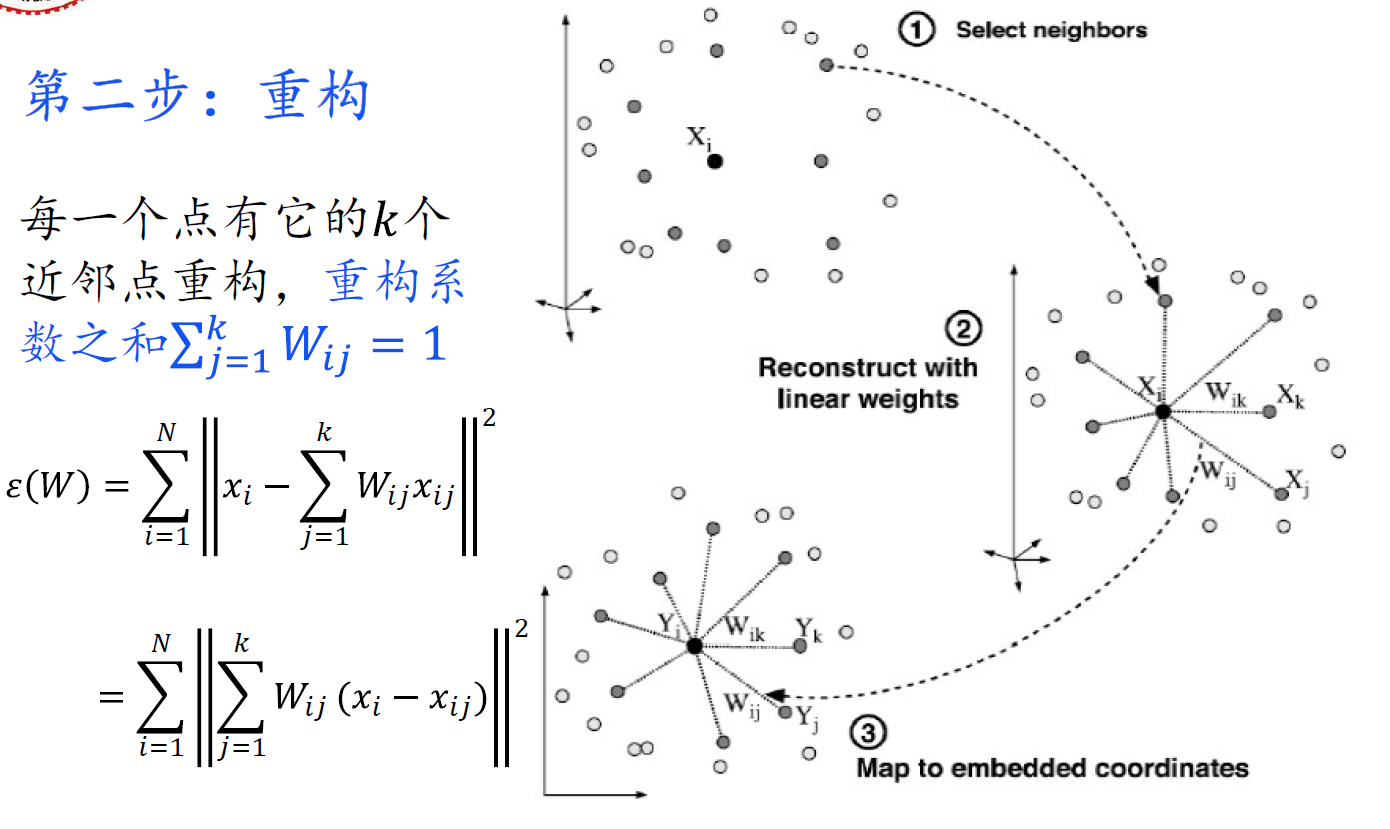
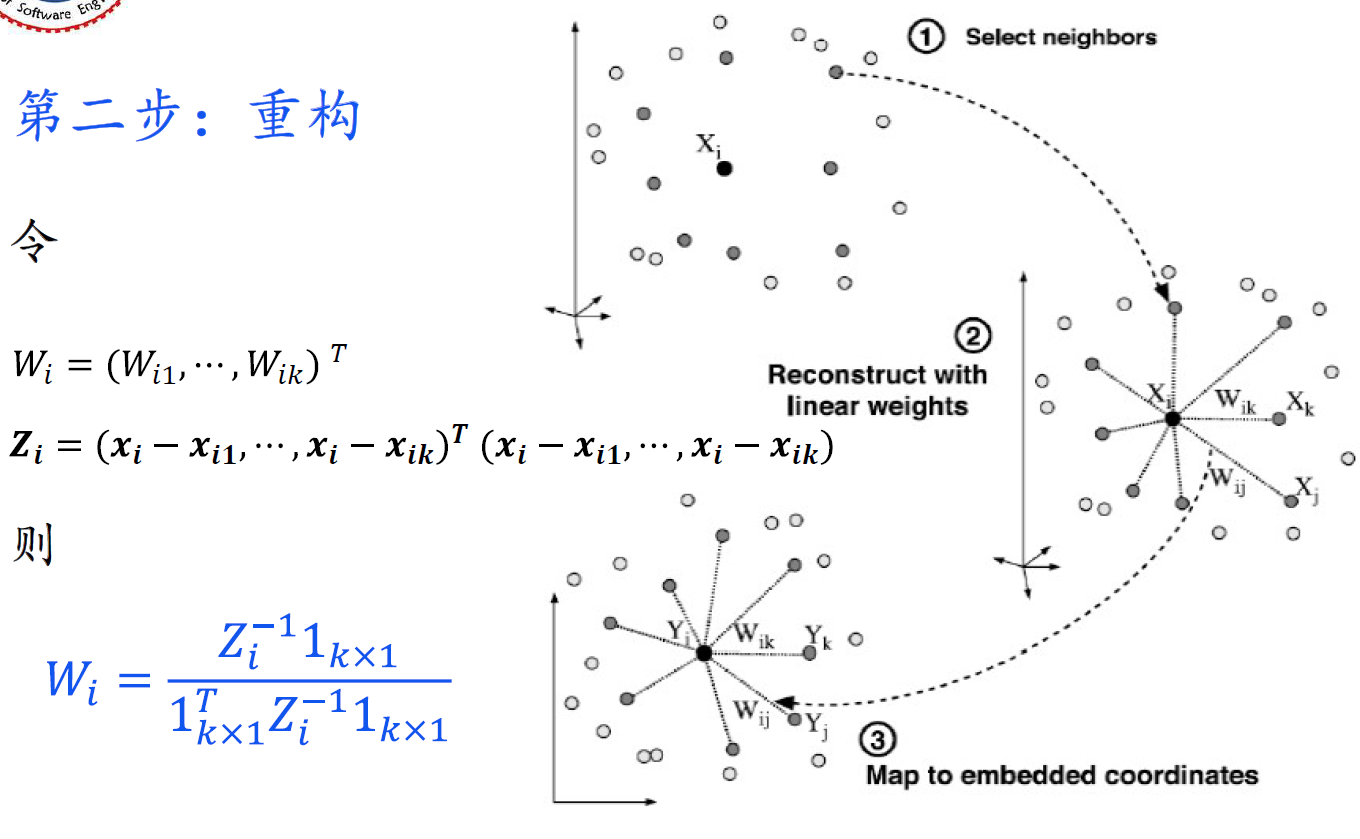
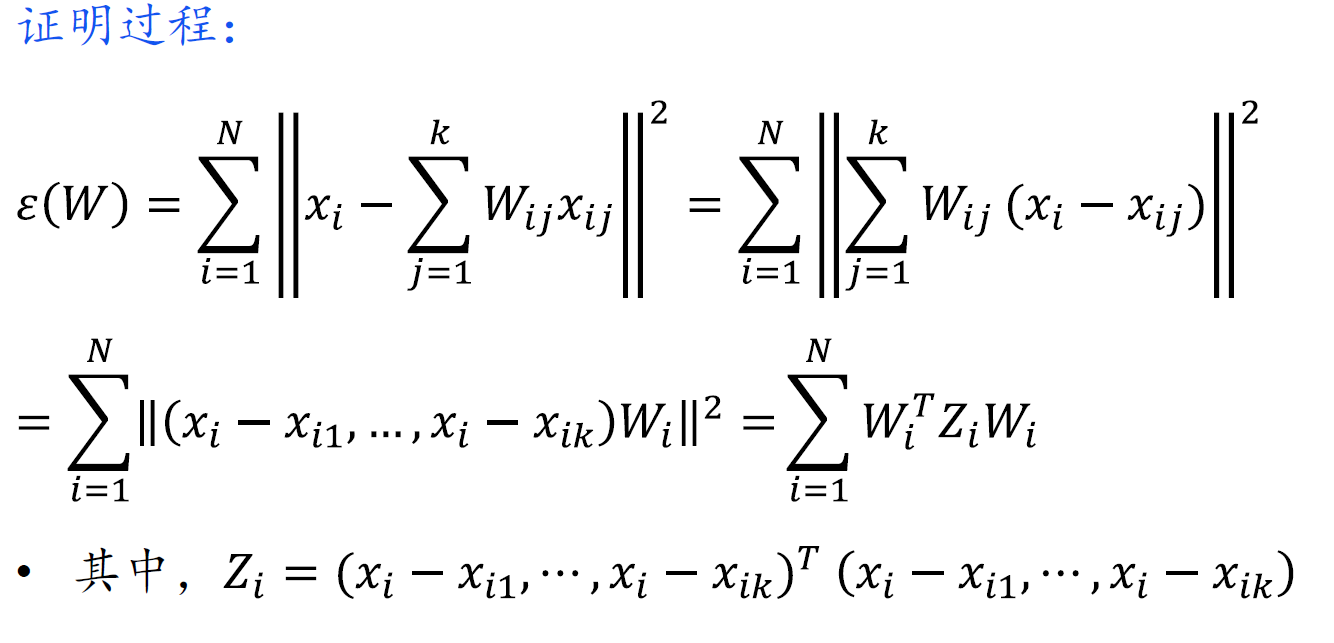

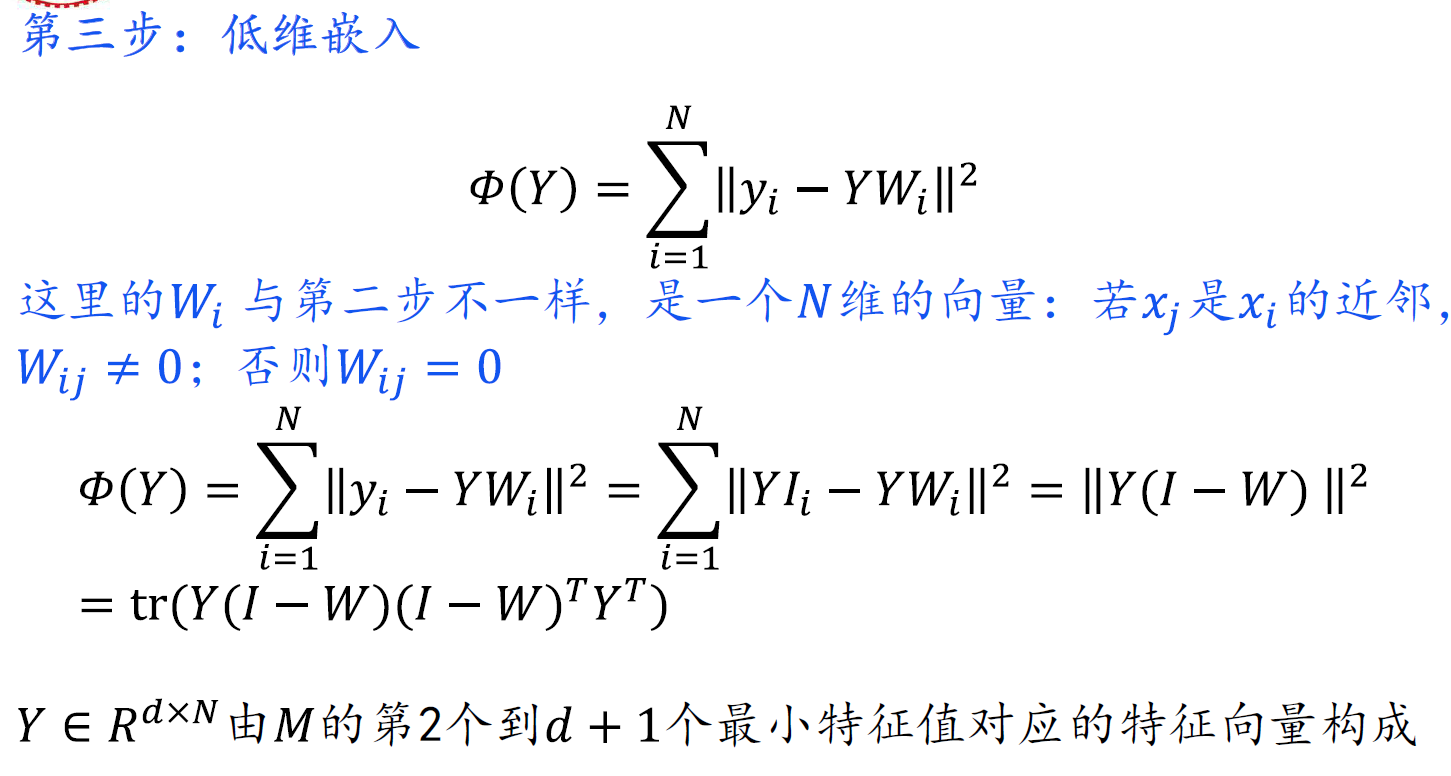


t-SNE


